| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- r-cnn
- eecs 498
- 그래프 이론
- dynamic programming
- hm3d
- CNN
- ubuntu
- GIT
- image processing
- MySQL
- 머신러닝
- 딥러닝
- Reinforcement Learning
- deep learning
- BFS
- AlexNet
- LSTM
- 백준
- C++
- 강화학습
- opencv
- Python
- real-time object detection
- hm3dsem
- YoLO
- RL
- DP
- dfs
- NLP
- machine learning
- Today
- Total
JINWOOJUNG
[ 영상 처리 ] Part2-3. OpenCV Mask Processing(C++) 본문
Before This Episode
다양한 Mask Processing에 대해 알아보고, 결과를 분석 해 보자.
영상에서 Noise를 제거하는 가장 기본적인 방법으로 Gaussian Filter에 대해서 배웠다. 일반적인 상황에서 발생되는 Noise는 Gaussian Distribution을 따른다. 따라서 Gaussian Noise를 제거하는 즉, 일반적인 Noise를 제거하는 최적 필터가 Gaussian Filter임이 증명되었다. 하지만 모든 Noise는 Gaussian Distribution을 따르지 않는다.


위와 같이 Salt-and-Pepper의 경우 Gaussian Filter를 통해 Noise를 제거한 결과 이상적이지 않는다. Salt-and-Pepper와 같이 Intensity가 튀는 Noise의 경우 오히려 주변으로 더 확산됨을 확인할 수 있다. 이러한 Noise를 제거하는 방법을 살펴보자
Median Filtering
Median Filter는 Kernel내의 Intensity의 중심 값을 특정 Pixel의 Intensity로 설정한다.

Salt-and-Pepper Noise의 경우 Intensity 값이 확 튄다. 위 Kernel 내의 Intensity 분포를 보면 Filtering을 적용하는 픽셀의 Intensity인 90의 경우 주변 픽셀의 Intensity에 비해 확 튐을 알 수 있다. 이러한 Intensity를 Fitering하기 위해, Median Filtering은 중간 값인 27을 Filtering을 적용하는 픽셀의 Intensity로 바꾼다. 중간 값에는 이러한 확 튀는 Noise 등이 올 확률이 더 적기 때문이다.
어떻게 보면 Salt-and-Pepper는 Noise라기 보다는 Outlier에 가깝다. 영상 내에서 특정 Kernel 내의 평균적인 Intensity 분포를 따르지 않는 Outlier이다. 따라서 이러한 Noise의 경우 Median Filtering이 효과적이다.
그렇다면 다음 질문을 생각 해 보자.
Is Median Filtering Linear?
Linear 즉, 선형적이다는 의미는 아래 조건을 만족해야 한다.
$$f(x \pm y) = f(x) \pm f(y)$$
$$f(kx) = kf(x)$$
하지만, Median Filtering은 Kernel 내의 Intensity들을 정렬하여 중간값을 취하는 과정을 동반하기 때문에 Linear하지 않다.
구현해보자.
DoMedianFiltering()
void DoMedianFiltering(const Mat& st_OriginalImage, Mat& st_ResultImage, int32_t s32_Size)
{
// Original Image가 없거나, Median 추출을 위한 s32_Size가 홀수인 경우 예외처리
if (st_OriginalImage.empty() || s32_Size % 2 == 0)
return;
st_ResultImage = Mat::zeros(st_OriginalImage.size(), CV_8UC1);
int32_t s32_Width, s32_Height, s32_KernelWidth, s32_KernelHeight;
// 가장자리 문제를 해결하기 위해 이미지의 유효한 범위 내에서만 Median Filtering을 실시
int32_t s32_HalfSize = s32_Size / 2;
for (s32_Height = s32_HalfSize; s32_Height < st_OriginalImage.rows - s32_HalfSize; s32_Height++)
{
for (s32_Width = s32_HalfSize; s32_Width < st_OriginalImage.cols - s32_HalfSize; s32_Width++)
{
vector<uchar> st_ValidIntensity;
// 현재 픽셀 기준으로 Median을 추출할 범위 내의 Pixel Intensity를 저장, 현재 픽셀이 해당 범위(Kernel)의 중심
for (s32_KernelHeight = -s32_HalfSize; s32_KernelHeight <= s32_HalfSize; s32_KernelHeight++)
{
for (s32_KernelWidth = -s32_HalfSize; s32_KernelWidth <= s32_HalfSize; s32_KernelWidth++)
{
st_ValidIntensity.push_back(st_OriginalImage.at<uchar>(s32_Height + s32_KernelHeight, s32_Width+s32_KernelWidth));
}
}
// Median Intensity 추출 후 결과 이미지에 할당
sort(st_ValidIntensity.begin(), st_ValidIntensity.end());
st_ResultImage.at<uchar>(s32_Height, s32_Width) = st_ValidIntensity[st_ValidIntensity.size() / 2];
}
}
}
하나하나 살펴보자.
// Original Image가 없거나, Median 추출을 위한 s32_Size가 홀수인 경우 예외처리
if (st_OriginalImage.empty() || s32_Size % 2 == 0)
return;
st_ResultImage = Mat::zeros(st_OriginalImage.size(), CV_8UC1);
int32_t s32_Width, s32_Height, s32_KernelWidth, s32_KernelHeight;
// 가장자리 문제를 해결하기 위해 이미지의 유효한 범위 내에서만 Median Filtering을 실시
int32_t s32_HalfSize = s32_Size / 2;
Median Filtering은 중앙값을 추출해야 하기 때문에 Kernel의 Size가 홀수여야 한다. 따라서 원본 이미지가 없거나 Kernel Size가 홀수가 아닌 경우 예외처리 하였다.
이전 포스팅에서는 가장자리 문제를 조건문을 걸어 해결하였다. 하지만, Kernel의 Size를 알고있는 상황에서 원본 이미지의 픽셀에 접근하는 Index에서 해당 문제를 해결하기 위해 Kernel Size의 절반인 s32_HalfSize를 선언하였다.
for (s32_Height = s32_HalfSize; s32_Height < st_OriginalImage.rows - s32_HalfSize; s32_Height++)
{
for (s32_Width = s32_HalfSize; s32_Width < st_OriginalImage.cols - s32_HalfSize; s32_Width++)
{
vector<uchar> st_ValidIntensity;
// 현재 픽셀 기준으로 Median을 추출할 범위 내의 Pixel Intensity를 저장, 현재 픽셀이 해당 범위(Kernel)의 중심
for (s32_KernelHeight = -s32_HalfSize; s32_KernelHeight <= s32_HalfSize; s32_KernelHeight++)
{
for (s32_KernelWidth = -s32_HalfSize; s32_KernelWidth <= s32_HalfSize; s32_KernelWidth++)
{
st_ValidIntensity.push_back(st_OriginalImage.at<uchar>(s32_Height + s32_KernelHeight, s32_Width+s32_KernelWidth));
}
}
// Median Intensity 추출 후 결과 이미지에 할당
sort(st_ValidIntensity.begin(), st_ValidIntensity.end());
st_ResultImage.at<uchar>(s32_Height, s32_Width) = st_ValidIntensity[st_ValidIntensity.size() / 2];
}
}
항상 Kernel의 중심에는 Mask Processing을 적용할 픽셀이 온다는 점을 기억하자.
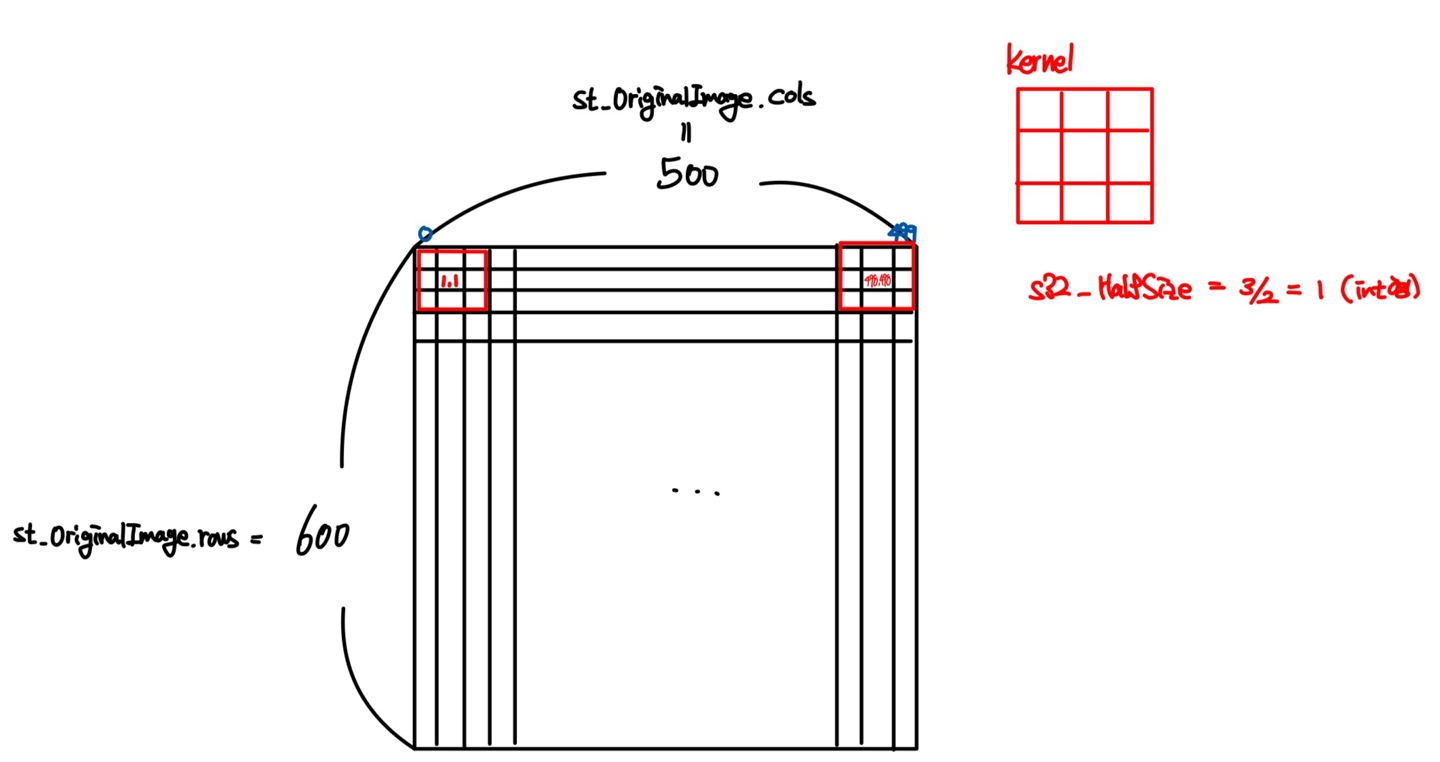
Mat::cols는 Mat 객체의 Width, Mat::rows는 Mat 객체의 Height를 나타낸다. 또한, 이미지는 2차원 배열이고, 각 픽셀에 접근하는 과정에서 Index는 0부터 시작한다. 따라서 Width를 예로 들면 0~499의 Index를 가진다.
가장자리 문제를 우리는 Median Filtering을 적용할 픽셀에 접근하는 과정에서 해결하고자 한다. Kernel Size가 3이라고 하면, 가장 먼저 적용 가능한 픽셀의 위치는 $(1,1)$이다. 즉, Kernel Size의 절반보다 큰 Index 부터 시작 가능하다. 이는 Mask Processing을 적용할 픽셀이 항상 Kernel의 중심에 위치해야 하기 때문이다. 또한, 가장 마지막으로 적용 가능한 Width의 최대값의 Index는 위 상황에서는 498이다. 즉 Mat::cols에서 Kernel Size의 절반을 뺀 Index 전까지 적용 가능하다. Height 역시 동일하다.
이를 코드적으로 표현하면 다음과 같다.
for (s32_Height = s32_HalfSize; s32_Height < st_OriginalImage.rows - s32_HalfSize; s32_Height++)
{
for (s32_Width = s32_HalfSize; s32_Width < st_OriginalImage.cols - s32_HalfSize; s32_Width++)
{
}
}
Median Filtering을 적용할 픽셀의 Index를 알았으면, 이제는 Kernel Size 만큼의 주변 Pixel의 Intensity 정보를 취득해야 한다. 이때, Index는 지난 포스팅에서 Convolution을 위한 Index 접근 방식을 사용한다. 인접 픽셀에 접근해서 해당 픽셀의 Intensity를 vector에 저장한다. 이때, Mat::at()으로 접근하기 때문에 $(height, width)$의 순으로 접근해야 함을 주의하자.
// 현재 픽셀 기준으로 Median을 추출할 범위 내의 Pixel Intensity를 저장, 현재 픽셀이 해당 범위(Kernel)의 중심
for (s32_KernelHeight = -s32_HalfSize; s32_KernelHeight <= s32_HalfSize; s32_KernelHeight++)
{
for (s32_KernelWidth = -s32_HalfSize; s32_KernelWidth <= s32_HalfSize; s32_KernelWidth++)
{
st_ValidIntensity.push_back(st_OriginalImage.at<uchar>(s32_Height + s32_KernelHeight, s32_Width+s32_KernelWidth));
}
}
이후 우리는 Median Intensity를 찾고 이를 Median Filtering을 적용할 픽셀의 Intensity로 설정하면 된다.
// Median Intensity 추출 후 결과 이미지에 할당
sort(st_ValidIntensity.begin(), st_ValidIntensity.end());
st_ResultImage.at<uchar>(s32_Height, s32_Width) = st_ValidIntensity[st_ValidIntensity.size() / 2];


결과를 보면 Median Filtering을 통해 Outlier를 잘 제거한 것을 확인할 수 있다. 이는 cv::medianBlur()와 동일한 결과를 보인다.
하지만, Kernel Size가 3인 경우 약간의 Outlier가 여전히 존재함을 알 수 있다. 해당 부분의 원본 이미지를 보면 해당 Outlier가 해당 픽셀 주변에 많이 분포함을 알 수 있다. Median Filtering은 결국 Kernel 내의 픽셀 Intensity의 중간값을 취득하는 과정이다. 만약 Kernel 내에 Outlier가 많이 분포한다면, 중간값 역시 Outlier가 되기에 정확히 Filtering이 되지 않을 수 있다.
이는 Kernel Size를 늘림으로써 해결할 수 있다. 동시에, 중간 값을 찾기위해 고려하는 인접 픽셀의 수도 증가하기에, Blur 효과도 커짐을 확인할 수 있다.
Gaussian Filtering
이전에 학습한 Gaussian의 적용 결과이다.

Gaussian Filtering 결과 Noise가 제거되는 효과도 있지만 위와 같이 Edge 부분 역시 없어짐을 확인할 수 있다. Gaussian Kernel을 살펴보면 각 부분에서 동일한 Kernel이 적용됨을 알 수 있는데, 이는 Kernel의 중앙 픽셀로부터 떨어져 있는 거리만을 고려하기 때문이다.
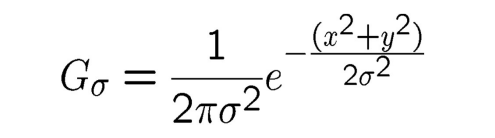
Edge는 하나의 Feature이기 때문에 없어지는 것은 치명적이다. 따라서 이를 보완하기 위한 Bilateral Filtering을 알아보자.
Bilateral Filtering

Gaussian Filtering과 달리 Kernel이 각 부분에 대해서 다른것을 확인할 수 있다. 이것이 Bilateral Filter이다.
상단의 일부 이미지처럼 단조로운 부분에 대해서는 기존과 동일한 Gaussian Filter가 적용된다. 하지만 두번재 일부 이미지와 같이 Edge가 있는 부분 즉, 픽셀 Intensity 차이가 큰 곳은 Kernel Weight가 0으로 없어짐을 알 수 있다. 마지막 역시 Intensity가 차이가 나는 곳은 Kernel Weight가 없어짐을 확인할 수 있다.
다시 말하면, Filter는 원래 픽셀 Intensity에 근거하여 새롭게 형성되다는 의미이다. 이는 수식적으로 보면 더 직관적으로 알 수 있다.

주황색 부분은 기존의 Gaussian의 수식과 동일하다. 즉, Kernel의 중심 픽셀로부터 떨어진 거리에 따라 Weight가 부여된다. 새롭게 추가된 부분은 Intensity 즉, 픽셀의 화소값을 고려한다. 따라서 Edge 부분은 Intensity의 차이가 크기 때문에, Weight가 줄어드는 것이다. 또한, Normalizatin Factor가 추가되었는데, 이는 단순히 Kernel Weight의 합으로 나눠주는 작업이다.
결국 Gaussian은 Filtering하는 Kernel의 중심 픽셀과 가까운 곳에 더 큰 가중치를, Range Weight는 중심 픽셀의 Intensity와 유사한 곳에 더 큰 가중치를 부여한다.

Bilateral Filter를 도식화 하면 다음과 같다. 왼쪽 위의 Filter는 Gaussian이고, 오른쪽 위는 Range Weight이다. 따라서 두 Weight를 모두 반영한 Filter가 Bilateral Filter이다. 따라서 Output을 보면, Edge 부분을 보존하고 있음을 알 수 있다.
구현해보자.
myBilateral()
void myBilateral(const Mat& src_img, Mat& dst_img, int diameter, double sig_r, double sig_s) {
Mat guide_img = Mat::zeros(src_img.size(), CV_64F);
dst_img = Mat::zeros(src_img.size(), CV_8UC1);
int wh = src_img.cols; int hg = src_img.rows;
int radius = diameter / 2; // 결국 diameter가 Kernel Size를 의미함
for (int c = radius; c < hg - radius; c++) {
for (int r = radius; r < wh - radius; r++) {
bilateral(src_img, guide_img, c, r, diameter, sig_r, sig_s);
}
}
// CV_64F로 높은 Intensity Resolution을 가지는 것을 다시 변환시킴
// 현제 거리 및 빛의 차이 두가지를 모두 고려하기 때문에 더 정밀도 있는 연산 결과 처리를 반영
guide_img.convertTo(dst_img, CV_8UC1); // Mat type변환
}
diameter는 Kernel size를 의미하고, sig_r은 Range Weight의 Sigma, sig_s는 Space Weight의 Sigma를 의미한다.
Bilateral Filtering 과정을 거치기 때문에 Intensity Resolution을 64바이트로 증가시켜 Intensity를 더 구체적으로 표현할 수 있도록 하였다. 이후 Mat::convertTo()를 통해 GrayScale, 8바이트 Mat 객체로 변환시킨다.
가장자리 문제를 고려하여 이중 for문 내에서 Bilateral Filtering을 적용할 픽셀에 접근한 후 bilateral()를 호출한다.
bilateral()
void bilateral(const Mat& src_img, Mat& dst_img, int c, int r, int diameter, double sig_r, double sig_s) {
int radius = diameter / 2;
double gr, gs, wei;
double tmp = 0;
double sum = 0;
for (int kc = -radius; kc <= radius; kc++) {
for (int kr = -radius; kr <= radius; kr++) {
gr = gaussian((float)src_img.at<uchar>(c + kc, r + kr)
- (float)src_img.at<uchar>(c, r), sig_r);
gs = gaussian(distance(c, r, c + kc, r + kr), sig_s);
wei = gr * gs;
tmp += src_img.at<uchar>(c + kc, r + kr) * wei;
sum += wei;
}
}
dst_img.at<double>(c, r) = tmp / sum;
}
Kernel 내의 모든 픽셀에 접근하여 Space Weight, Range Weight를 계산한다. Range Weight의 경우 두 픽셀의 Intensity Difference가 gaussian()의 인자가 되기 때문에, Mat::at()을 통해 접근함을 알 수 있다. Space Weight의 경우 두 픽셀의 떨어진 거리가 인자가 되기 때문에 해당 픽셀의 Index를 distance()의 인자로 하여 거리를 계산하고, 이를 gaussian()의 인자로 하여 Weight를 계산한다.
distance()
float distance(int x, int y, int i, int j) {
return float(sqrt(pow(x - i, 2) + pow(y - j, 2)));
}
단순히 두 픽셀 사이의 거리를 계산하는 함수이다.
gaussian()
double gaussian(float x, double sigma) {
return exp(-(pow(x, 2)) / (2 * pow(sigma, 2))) / (2 * CV_PI * pow(sigma, 2));
}
Gaussian Function 수식에 근거한 연산 과정이다.
이렇게 계산한 두 Weight를 Bilateral Filter 수식에 근거하여 곱한 후 정규화를 시켜 Filtering 할 픽셀의 Intensity로 설정한다.

수행 결과 위와 같다. 왼쪽은 Space Sigma는 모두 1이고, 위에서 부터 아래로 Range Sigma는 2, 25, 50이다.
오른쪽은 Space Sigma는 모두 100이고, 위에서 부터 아래로 Range Sigma는 2, 25, 50이다.


동일한 Space Sigma에 대해서, Range Sigma가 클수록 Gaussian Filtering 처럼 전체적으로 Blur효과가 극대화 됨을 확인할 수 있다. 이는 Sigma가 커짐으로써 Intensity 차이가 많이 나는 픽셀에 대한 Weight가 Sigma가 적을 때보다 커지기 때문에 Edge를 잘 보존하지 못하고, 해당 픽셀의 평균값을 계산하는 과정에서 더 Intensity의 차이가 많은 픽셀의 Intensity도 고려되기 때문이다. 따라서 Range Sigma가 적을수록 Edge를 보존함을 확인할 수 있다. 이는 Intensity의 차이역시 Bilateral Filtering에서는 고려되기 때문에 해당 픽셀에 대한 Weight가 적어져 결국 평균화에 영향을 덜 주기 때문이다.
동일한 Range Sigma에 대해서, Space Sigma가 클수록 Blur 현상이 더 심해지는데, 이는 Bilater Filtering을 진행하는 픽셀로부터 거리가 먼 픽셀 역시 고려하기 때문에, 더 많은 부분이 평균화 되어 Blur현상이 심해진다.
Canny Edge Detection
Canny Edge Detection은 다양한 프로세스를 통해 Edge를 검출한다.
- Noise Reduction
- Gaussian Filter를 통한 Image Smoothing
- Intensity Gradient Calculation
- 수평, 수직 방향으로 Sobel Filter를 활용한 Gradient의 크기와 방향 계산
- 픽셀이 사각형이기 때문에 총 4개의 구역 설정
- Non-Maximum Suppression
- 모든 픽셀에 대해서 특정 픽셀의 Gradient가 인접 픽셀들의 Gradient의 최대값이 아니면 전부 0으로 설정
-> Edge에 따른 얇은 Edge를 추출, Edge가 두껍게 추출되는 Sobel Filter 보완
- 모든 픽셀에 대해서 특정 픽셀의 Gradient가 인접 픽셀들의 Gradient의 최대값이 아니면 전부 0으로 설정
- Double Thresholding and Edge Tracking by Hysteresis
- 최종적인 Edge를 선별하기 위해 $T_{max}, T_{Low}$ 설정
- $T_{max}$ 이상의 Gradient를 가지는 픽셀은 Edge로 판단
- $T_{Low}$ 이하의 Gradient를 가지는 픽셀은 Edge가 아닌 것으로 판단
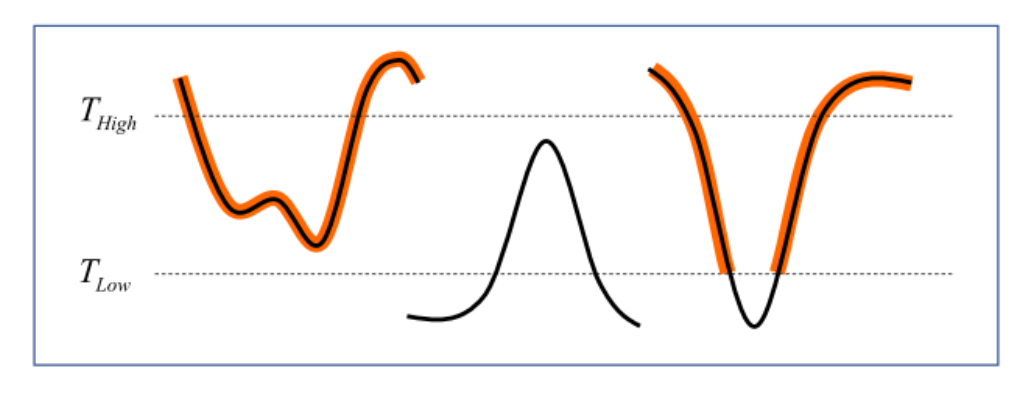
- 두 Threshold 사이의 Gradient를 가지는 픽셀을 이어갔을 때, $T_{max}$ 이상의 Gradient를 가지는 픽셀과 연결된다면 해당 구간의 픽셀을 모두 Edge로 판단
-> 조명, 햇빛 등 환경에 따른 엣지 검출 조건의 변화에 강건하게 하기 위함
OpenCV의 공식 문서를 통해 각 파라미터의 의미를 살펴보자

- image : 입력 이미지
- edges : 에지 검출 결과 이미지
- threshold1 : Low Threshold
- threshold2 : Max Threshold
- apertureSize : Sobel Filter Kernel Size
- L2gradient : True이면 L2 norm, False이면 L1 norm 사용
마지막 L2gradient Parameter의 경우 Sobel Filter로 추출한 Gradient의 크기를 계산할 때 사용된다.
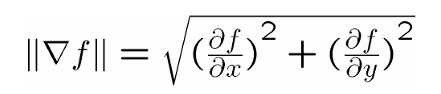
이때, L1 norm은 단순히 각 Gradient의 절댓값을 더한다. 하지만 L2 norm은 위 식과 같이 Gradient의 제곱 합에 루트를 씌운 구조이다.
인공지능에서 사용되는 손실함수로써의 L1, L2 norm은 L2가 L1 보다 Outlier에 더 강한 반응을 보임을 알 수 있는데, 여기서는 그 의미는 아닌 것 같고 그저 수식적으로 이해하고 넘어가자.
OpenCV의 cv::Cany()는 쉽게 적용 가능하다.
Mat st_OriginalImage = imread("rock.png", 0);
cv::Canny(st_OriginalImage, st_CannyEdge, 0, 300, 3);
각각의 cv::Canny()의 동작속도는 다음과 같이 측정할 수 있다.
#include <time.h>
clock_t start, finish;
start = clock();
cv::Canny(st_OriginalImage, st_CannyEdge, 100, 300, 3, false);
finish = clock();
cout << "Duration : " << (double)(finish - start) << endl;
각각의 파라미터를 변환 해 가면서 결과를 분석 해 보자.
1. Min Threshold
cv::Canny(st_OriginalImage, st_CannyEdge, 20, 250, 3);
cv::Canny(st_OriginalImage, st_CannyEdge2, 100, 250, 3);
cv::Canny(st_OriginalImage, st_CannyEdge3, 200, 250, 3);
Min Threshold가 줄어들수록 바위 내부, 나무에서 더 작은 Gradient 차이를 보이는 Week Edge들도 검출되는 것을 확인할 수 있다.
각각은 24ms, 9ms, 7ms의 동작속도가 걸렸는데, 이는 Min Threshold가 커질수록 Edge가 아니라고 판단되는 Gradient의 강도가 더 높아지기 때문에 더 적은 Edge가 검출되기 때문이다.
2. Max threshold
cv::Canny(st_OriginalImage, st_CannyEdge, 50, 100, 3);
cv::Canny(st_OriginalImage, st_CannyEdge2, 50, 200, 3);
cv::Canny(st_OriginalImage, st_CannyEdge3, 50, 300, 3);
Max Threshold가 커지면 Edge라고 판단되는 기준이 더 엄격해진다. 따라서 바위 내부의 Edge들이 Max Threshold가 커지면서 점점 줄어드는 것을 확인할 수 있다.
각각은 28ms, 11ms, 8ms의 동작속도가 걸렸는데, 이는 Max Threshold가 더 줄어들수록 실제로 Edge라고 판단되는 Gradient의 강도가 낮아지기 때문에 더 많은 Edge가 검출되기 때문이다.
3. Kerene Size
cv::Canny(st_OriginalImage, st_CannyEdge, 0, 300, 3);
cv::Canny(st_OriginalImage, st_CannyEdge2, 200, 300, 3);
cv::Canny(st_OriginalImage, st_CannyEdge3, 200, 300, 5);
동일한 조건에서 Min Threshold가 낮아지면 Edge로 판단하는 기준이 완화해져 Week Edge 즉, Gradient의 크기가 작은 Edge도 검출되는 것을 2,3번째 이미지를 비교하면 바위 윗 부분도 Edge가 검출되는 것에서 확인할 수 있다.
동일한 조건에서 Kernel Size를 3에서 5로 변화하면, Sobel Filter에서 Edge를 검출하는데 판단하는 Kernel의 크기가 더 커져 더 많은 픽셀을 고려하여 Edge를 검출하게 된다. 따라서 3x3 Kerenel 에서는 Low Threshold 보다 작아 Edge로 분류가 되지 않은 Edge 역시, Kerenel Size가 커지면서 더 많은 픽셀 Intensity를 살펴봤을 때 Edge로 판단되고 그에 따른 Gradient 크기가 커져 Edge로 검출됨을 3,4번째 이미지에서 확인할 수 있다.
동작속도는 각각 23ms, 6ms, 19ms이다. 1,2번째의 Canny Edge Algorithm의 차이는 Min Threshold이다. Max Threshold는 동일하지만, 첫번째의 경우 Min Threshold가 0이기에 Max Threshold 보다 작은 Gradient 강도를 가지는 Edge들이 Max Threshold 이상의 Gradient 강도를 가지는 픽셀들과 연동되어 더 많은 Edge들이 검출되기 때문이다.
2,3번째 Canny Edge Algorithm의 차이는 Kernel Size이다. Kernel Size가 커질수록 실제로 Mask Filtering을 적용시킬 수 있는 픽셀수는 적어지지만, Sobel Filter를 적용시키는 픽셀들의 범위가 더 넓어지기 때문에 더 작은 Edge들이 검출될 확률이 높아진다. 따라서 더 많은 연산 속도가 요구된다.
4. L1, L2 Norm
cv::Canny(st_OriginalImage, st_CannyEdge, 100, 300, 3, false);
cv::Canny(st_OriginalImage, st_CannyEdge2, 100, 300, 3, true);
L1 norm은 대각선의 Gradient 변화량(크기)를 계산함에 있어서 부정확하다. 단순히 그 크기를 더하기 때문에, 정확히 유클리디안 거리를 사용하여 크기를 계산하는 L2 norm에 비해 부정확하다. 위 Edge 검출 결과로 L1 norm이 부정확한(Week Edge)를 더 많이 검출함을 확인할 수 있다.
이는 동작속도에서도 확인 가능한데 L1은 22ms가 걸린 반면, L2는 9ms의 동작속도를 보인다. 이는 L1이 부정확한 Edge를 더 많이 검출하기 때문에 해당 과정에서 더 많은 연산이 요구되기 때문이다.
'2024 > Study' 카테고리의 다른 글
| [ 영상 처리 ] Ch4. Edge Detection (0) | 2024.04.11 |
|---|---|
| [ 영상 처리 ] Ch3. Mask Processing(Filtering in Spatial Domain) (0) | 2024.04.11 |
| [ 영상 처리 ] Part2-1. OpenCV Mask Processing(C++) (0) | 2024.04.07 |
| [ 영상 처리 ] Part1-2. OpenCV Image Processing(C++) (0) | 2024.04.06 |
| [ 영상 처리 ] Part1-1. OpenCV Image Processing(C++) (0) | 2024.04.06 |




