| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- DP
- AlexNet
- BFS
- machine learning
- image processing
- UC Berkeley
- Python
- 딥러닝
- CS285
- ubuntu
- opencv
- 강화학습
- Reinforcement Learning
- GIT
- dynamic programming
- hm3d
- RL
- dfs
- YoLO
- MySQL
- r-cnn
- NLP
- 그래프 이론
- 백준
- C++
- LSTM
- 머신러닝
- CNN
- deep learning
- hm3dsem
- Today
- Total
JINWOOJUNG
[ 영상 처리 ] Ch9. Local Feature Detection and Matching(4) 본문
본 영상 처리 개념과 기법들에 대한 공부를 진행하면서 배운 내용들을 중심으로 정리한 포스팅입니다.
책은 Computer Vision: Algorithms and Applications를 기반으로 공부하였습니다.
또한, 인하대학교 박인규 교수님의 디지털 영상 처리 과목을 기반으로 제작된 포스팅입니다.
Before This Episode
[ 영상 처리 ] Ch9. Local Feature Detection and Matching(3)
본 영상 처리 개념과 기법들에 대한 공부를 진행하면서 배운 내용들을 중심으로 정리한 포스팅입니다. 책은 Computer Vision: Algorithms and Applications를 기반으로 공부하였습니다.또한, 인하대학교 박
jinwoo-jung.com
이전 포스팅에서는 Scale에 불변하는 SIFT의 기본이 되는 원리를 소개하였다. 이제 SIFT에 대하여 구체적으로 알아보자.
SIFT

SIFT는 Scale Invariant Feature Transform의 약자로, 말 그대로 Scale에 불변하는 특징 추출을 위한 변환을 의미한다. 아래 그림에서 왼쪽은 원본 이미지, 오른쪽은 트럭이 Scale, View Point 변환으로 인한 Rotation이 나타남을 알 수 있다. SIFT는 Local Feature를 추출하고 Normalized Descriptor로 변환하여 Scale에 불변하는 Feature를 추출한다.


지난 포스팅에서 한 이야기를 잠깐 다시 해 보겠다. 원본 영상에서의 Local Feature는 Scale이 변화된 이미지에서 동일한 크기의 Patch를 고려한다면, 동일한 Feature에 대해서도 Description의 차이가 존재하여 Feature Matching이 불가하다. 하지만, 오른쪽과 같이 Scale에 따른 Patch의 크기가 달라진다면 즉, Scale이 고려된다면, Scale에 불변한 Local Feature를 추출할 수 있다.
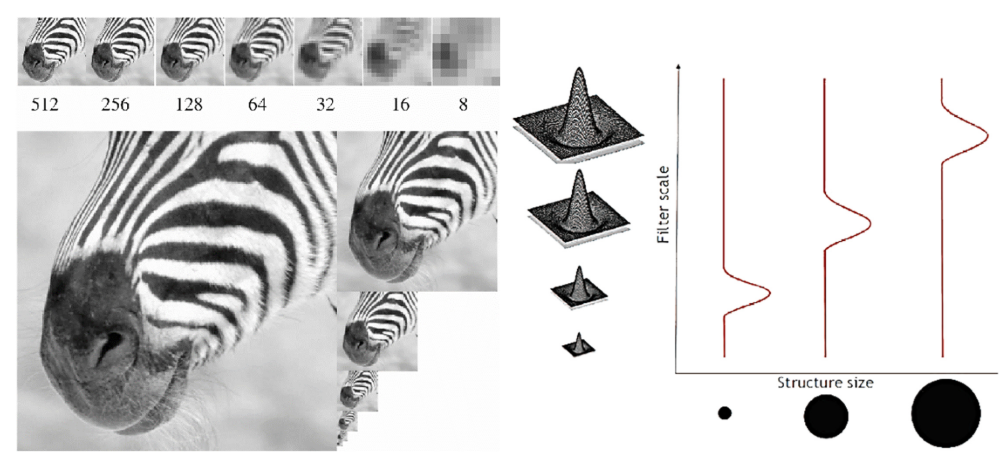
따라서, LoG를 $f$로 하여 blob을 추출 하였다. blob은 Local Feature의 가능성이 있는 Location과 Scale을 의미하는 $\sigma$를 포함한다.

SIFT의 첫번째 아이디어가 등장하는데, 바로 연산량이다. blob Detection을 위한 LoG의 $\sigma$를 변화시켜 가면서 Filtering을 하는 과정은, $\sigma$가 커질수록 많은 연산량이 요구된다. 따라서 $\sigma$를 무작정 키우는 것이 아닌, 일정한 증가가 이루어 진다면, 영상의 크기를 축소시켜 연산량을 감소시키는 것이다.
오른쪽 LoG의 $\sigma$에 따른 영상의 크기를 살펴보자. 여기서 Octave라는 개념이 나오는데, 이는 영상의 크기가 동일한 집단을 의미한다. 한 Octave에 현재는 5개의 영상이 존재한다. 그리고 다음 Octave로 넘어가면서 영상의 Size가 $\frac{1}{2}$가 되어 전체 크기는 $\frac{1}{4}$가 된다. 이때, 이전 Octave에서 사용한 $\sigma$ 값이 재사용 되면서 점진적으로 $\sigma$값이 커져 연산량이 과도하게 커지는 것을 막아준다.
이때, $k$는 $2^{\frac {1}{s}}$인데, 이때 $s$는 한 옥타브의 간격의 수로, 현재 한 옥타브에 5개의 영상이 존재하기에 $s =4$이다.

SIFT의 두번째 아이디어는 LoG를 DoG로 근사시켜 계산하는 것이다.
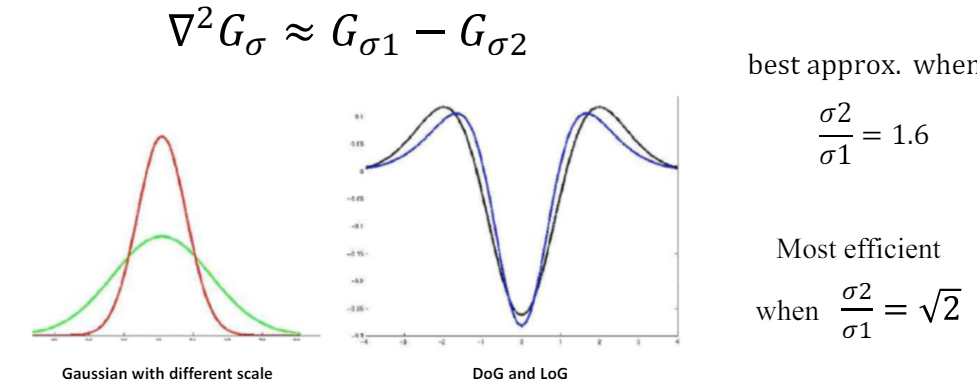
가운데 DoG와 LoG의 그래프를 보면 매우 유사함을 확인할 수 있다. 따라서, LoG를 DoG로 근사시켜 사용하는데, 이때 인접한 두 층의 $\sigma$의 비율인 $\frac{\sigma2}{\sigma1}$가 $\sqrt{2}$인 경우 가장 효과적이기에 인접한 두 층의 $sigma$의 비율이 $\sqrt{2}$로 설정된다.


이렇게 추출된 Local Feature의 가능성이 있는 keypoint들에 대하여 3차원 NMS를 적용하여 Local Maximum을 추출한다. keypoint를 기준으로 8개의 Pixel, 인접한 두 층의 동일한 영역의 9개의 Pixel 총 26개의 Pixel에 대하여 NMS를 적용하면 된다. 하지만, 이 역시 수많은 연산과 비교가 이루어 지기 때문에 많은 연산량이 요구된다. 따라서 Keypointd의 위치를 정확하게 하기 위한 다른 접근법이 등장한다.
SIFT - Keypoint Localization


일종의 예외처리라고 생각하자. 먼저 NMS로 추출된 Keypoint 중 인접픽셀과의 차이(대조)가 적은 경우는 제외시킨다. 예를들어 오른쪽과 같은 3차원 NMS가 적용되어 Keypoint로 가운데 층의 가운데 픽셀이 위치되었다고 하자. 물론 Local Maximum이 맞지만, 인접 픽셀과의 차이가 적기 때문에 Local Feature로는 부적절하다.
또한, Edge 상의 Keypoint를 제거하기 위해 hessian Matrix와 아래의 공식이 도입되었다. 너무 깊게는 들어가지 말고, Hessian Matrix의 det(), trace()의 비율을 기반으로 해당 Keypoint가 Edge상에 존재하는지 판단한다고만 기억하자.

Keypoint 추출 결과인데, 화살표의 방향과 크기는 무시하고, 화살표가 시작하는 위치인 Keypoint만 고려하자. NMS를 통해 추출한 keypoint가 Low Contrast, Edge 상의 Keypoint를 제거하니 536개로 유효한 Keypoint만 Localization 됨을 확인할 수 있다.
SIFT - Orentation Assignment
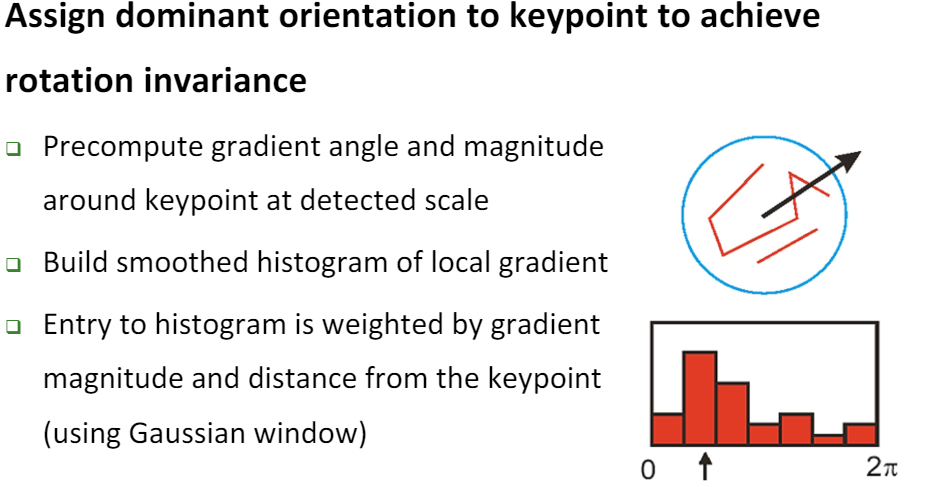
이때까지는 Keypoint의 크기와 Scale에 대한 불변성만 고려되었다. 하지만, Rotation에 대한 불변성도 확보해야 한다. 이제부터는 Keypoint의 Orientation 즉, 주된 방향을 결정 해 보자.
우리는 blob을 추출하였기에, 해당 Keypoint의 Scale 요소인 $\sigma$를 알고 있다. 따라서 Keypoint의 $\sigma$에 따른 범위 내의 Gradient와 Magnitude를 계산하고, Hog(Histogram of oriented Gradient)를 계산한다. 즉, 영역 내의 Gradient를 Count하여 가장 빈도수가 높은 Gradient를 해당 Keypoint의 Orientation으로 설정한다. 이때, Gradient Magnitude와 Keypoint와의 Distance에 따른 Weight를 부여하여 HoG를 계산한다. 따라서 Gaussian Window가 사용된다.

위와 같이 HoG가 계산되었다고 하자. 0~360 범위이기에 10씩 끊어서 계산한 결과이다. 20~29도가 가장 빈도수가 높기 때문에 해당 Keypoint의 Orientation으로 설정한다. 이때, Peak점 즉, 가장 높은 분포를 가지는 Orientation 빈도수의 80%를 넘기는 방향에 대해서도 또다른 Keypoint로 고려된다. 즉 하나의 Location에 대하여 서로 다른 Orientation을 가지는 서로 다른 Keypoint가 결정 될 수도 있다.

따라서 SIFT 결과 검출된 Keypoint는 오른쪽과 같다.
하지만, 이것만으론 Feature Matching을 진행하기 위해 각 Feature에 대한 정량화가 부족하다. 따라서 Descriptor 개념이 등장한다.
SIFT - Descriptor
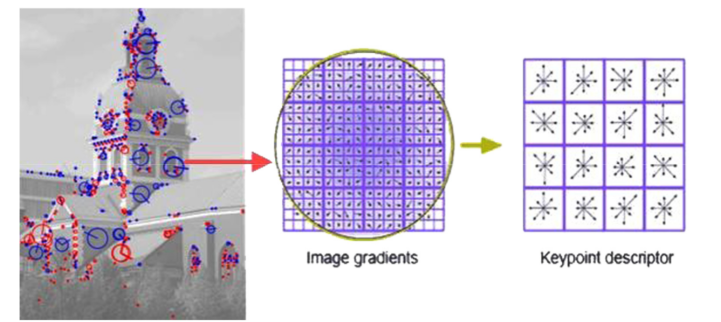
가운데 Image Gradients를 기반으로 우리는 앞서 Keypoint의 Orientation을 결정하였다. 하지만, 그것만으론 해당 Keypoint를 정량화 할 순 없다. 따라서 등장한 개념이 SIFT Descriptor이다. 먼저 Keypoint를 기준으로 16by16 Window를 생성한다. 이를 4by4로 Sub Region이 나눈다. 이후 16개의 작은 윈도우에 속한 Pixel들의 Gradient의 크기와 방향을 계산한 뒤 8개의 bin을 가지는 즉, 8 Orientation Histogram을 그린다.

따라서 16개의 Sub Region Window에 대하여 8개 방향 Orientation이 결정되기 때문에 최종적으로 128개의 Feature Vector를 가지는 Descriptor를 생성할 수 있다.
영상이 회전하면 모든 Gradient의 방향이 변화하기 때문에 Feature Vector도 변하게 된다. 따라서 Rotation이 적용된 영상의 경우 같은 Keypoint에 대한 Feature Vector는 영상이 Rotation 된 만큼 변하기 때문에 Matching에 어려움을 가진다. 따라서 Feaure Vector에서 Keypoint의 Orientation을 빼주면 즉, 16개의 각 윈도우에 대하여 Keypoint의 방향을 빼주게 된다면, 각 윈도우의 방향은 Keypoint에 대하여 상대적인 방향을 가지게 된다. 따라서 Roation에 불변성을 가지게 된다.

결국엔 SIFT Feature는 128차원의 Descriptors, Scale, Orientation, Location(2D Coordinates) 정보를 갖게 된다.
'2024 > Study' 카테고리의 다른 글
| [ 영상 처리 ] Ch8. Clustering and Segmentation(1) (0) | 2024.05.29 |
|---|---|
| [ 영상 처리 ] Ch7. Color Image Processing (0) | 2024.05.29 |
| [ 영상 처리 ] Ch9. Local Feature Detection and Matching(3) (0) | 2024.05.27 |
| [ 영상 처리 ] Ch9. Local Feature Detection and Matching(2) (0) | 2024.05.27 |
| [ 영상 처리 ] Ch9. Local Feature Detection and Matching(1) (1) | 2024.05.27 |




