| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- CS285
- deep learning
- Reinforcement Learning
- 머신러닝
- ubuntu
- NLP
- 그래프 이론
- MySQL
- C++
- machine learning
- opencv
- GIT
- 딥러닝
- DP
- UC Berkeley
- YoLO
- dfs
- RL
- LSTM
- hm3dsem
- AlexNet
- 백준
- hm3d
- 강화학습
- CNN
- Python
- BFS
- r-cnn
- image processing
- dynamic programming
- Today
- Total
JINWOOJUNG
Q-Learning 본문
본 게시글은 인하대학교 유상조 교수님의 Reinforcement Learning Tutorial Seminar
수강 후 정리를 위한 포스팅입니다.
모든 포스팅의 저작관은 유상조 교수님에게 있음을 사전 공지합니다.
Before This Episode
https://jinwoo-jung.tistory.com/31
State-Action-Reward-State-Action
본 게시글은 인하대학교 유상조 교수님의 Reinforcement Learning Tutorial Seminar 수강 후 정리를 위한 포스팅입니다. 모든 포스팅의 저작관은 유상조 교수님에게 있음을 사전 공지합니다. Before This Episode
jinwoo-jung.tistory.com
Q-Learning
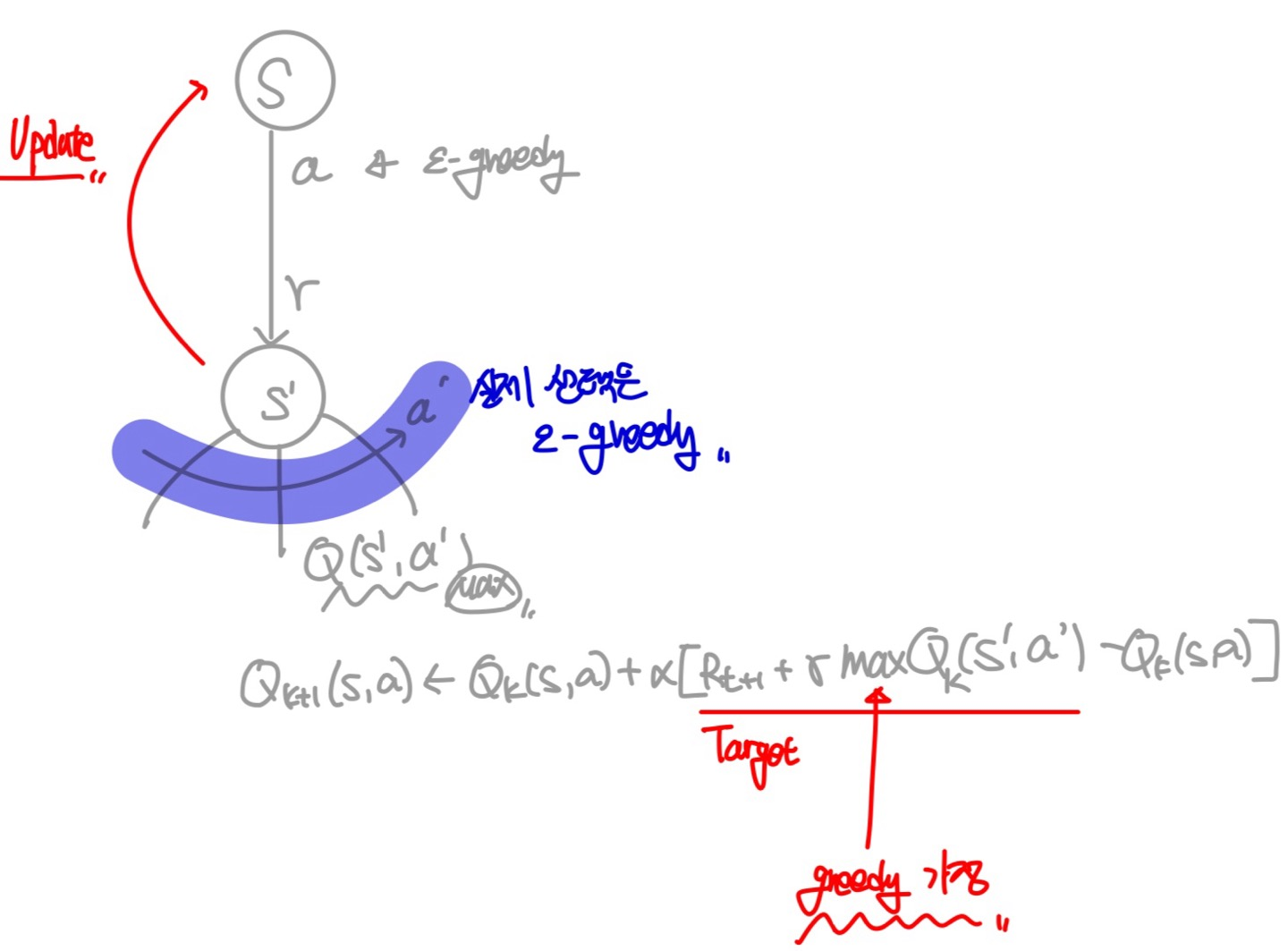
Q-Learning은 지난 시간에 언급한 것 처럼, Behavior Policy와 Target Policy가 다른 Off-Policy이다. SARSA처럼, $\varepsilon$-greedy에 의해 선택된 action $a$를 통해 state $S'$으로 이동 후 특정한 action $a'$를 수행했을 때의 action-value를 이용하여 update를 하는 것은 동일하나, 선택되어지는 action $a'$은 $Q_k(S',a')$이 가장 큰 action을 greedy하게 선택한다는 가정 하에 Target value가 계산된다. 하지만, 실제 action 선택은 $\varepsilon$-greedy에 의해 선택된다.
$$Q(S_t,a_t) \leftarrow Q(S_t,a_t) + \alpha {R_{t+1} + \gamma max_{a_{t+1}} Q(S_{t+1},a_{t+1})-Q(S_t,a_t)}$$
이렇게 Exploration을 하는 방법은 여러가지가 있는데, 정리하면 아래와 같다.

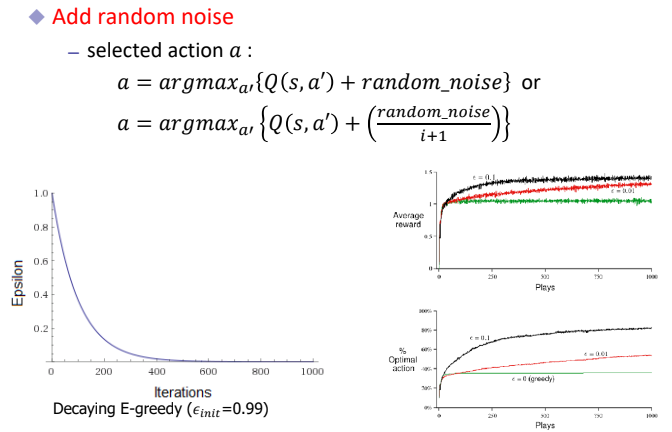
간단히 살펴보면, $\varepsilon$-greedy는 state-value가 가장 큰 action을 1- $\varepsilon$확률로 선택하고, $\varepsilon$ 확률로 random하게 action을 선택하는 방법이다. 이때, iteration이 증가될수록 Optimal Policy에 가까워져 Exploration의 필요성이 줄어들기 때문에 $\varepsilon$을 감소시켜 greedy하게 선택하는 방법이 Decaying E-greedy이다.
Boltzmann Exploration은 각 action-value에 비례하게 Exploration을 진행하는 방법이며, Add random noise는 Multi-Armed Bandit에서 배운 UCB처럼 noise를 주는 것이다.
Q-Learning Algorithm

Q-Learning Algorithm을 간단하게 살펴보면 초기 state를 random하게 설정하고 $Q(s,a)$도 초기화 시킨다. 이후 $\varepsilon$-greedy에 의해 action $a$를 선택하여 진행한 후 Reward $R$과 새로운 state $s_{new}$를 관측한다. 이후 $Q(s_{new},a')$이 가장 큰 $a'$을 이용하여 target value를 계산하여 $Q(s,a)$를 update 한다.


예시를 통해 Q-Learning을 이해 해 보자.
먼저 초기 state $s_1$에서 $\varepsilon$-greedy에 의해 action $a_1,a_2$ 중 $a_2$가 선택되어 졌다고 가정하자. 이때, action $a_2$로 인해 reward +3이 측정되었고, state는 $s_2$가 되었다. Q- Learning Update를 위해 $Q(s_2,a')$이 가장 크게 되는 action $a_3$가 선택되어지고, 이를 이용해 $Q(s_1,a_2)$ Update하면 왼쪽 식과 같이 계산되어 진다. 동일한 방법으론 오른쪽에서 $Q(s_2,a_3)$를 Update함을 알 수 있다.
그럼 Q-Learning과 SARSA의 큰 차이는 무엇일까?

Cliff Walking은 절벽으로 갈 때 Reward를 -100을 받고, 나머지는 모두 -1을 받는 예시이다.
Q-Learning은 탐험으로 인한 Reward를 고려하지 않는다. Update 과정에서 선택한 action에 의해 이동한 state에서 Q가 가장 큰 action을 선택하여 Update를 진행한다. 따라서 절벽으로 가는 action이 고려되지 않고, Goal로 가는 가장 빠른 action이 선택되어 진다.
On-Policy인 SARSA의 Update를 다시 살펴보면, $Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha [R_{t+1} + \gamma Q(S_{t+1},A_{t+1}) - Q(S_t, A_t)]$으로 실제 Behavior에 의한 Q를 이용해 Update를 진행한다. 따라서 절벽으로 가 -100의 Reward를 받는 상황 역시 고려되기에 절벽에서 먼 가장 안전한(Reward가 큰) 방향으로 action이 선택되어 진다.
수많은 Episode에 대하여 Rewards의 합 graph를 보면, SARSA가 더 크다는 것을 알 수 있다. 즉, Q-Learning은 절벽으로 갈 수 있기 때문에 더 낮다. 즉, Off Policy임을 다시한번 확인할 수 있다. 그렇다면 무조건 SARSA가 좋은 것일까?
| SARSA | Q-Learning |
| Q Update : $\varepsilon$-greedy Behavior | Q update : $Q(s', a)$가 최대가 되는 action 실제 Behavior는 $\varepsilon$-greedy |
| 다음 상태에서의 탐험을 고려 - Online Learning | 실제로 학습(탐험)을 고려 x, Just 학습이 된 것을 사용 - Offline Learning But 빠르게 Optimal Policy를 찾을 수 있음 |
Problems of TD Learning
TD의 한 종류인 SARSA, Q-Learning 모두 Maximization의 문제가 있다. Q-Learning은 $ max_{a_{t+1}} Q(S_{t+1},a_{t+1})$가 고려되고, SARSA의 경우 $\varepsilon$-greedy이지만 이 역시 maximization operation이 포함되어 있어 positive bias로 유도한다. 만약 Reward가 평균이 0인 양수/음수의 값이 모두 나온다면, 두 method 모두 항상 양수의 reward를 얻는 action을 취하게 된다. 이를 Maximizatino Bias라 한다.
이를 해결하기 위해 별도의 action-value functions의 value를 다루는 $Q$ 를 학습시키는 Double Q-Learning이 등장하였다.

먼저 예시를 통해 살펴보면, 위와 같이 두개의 $Q$를 학습시킨다. 이때, 한쪽 $Q$를 Update를 하기 위해 다른쪽 $Q$가 사용된다.
위 예시에서 state $s$에서 action $a$가 선택되어 $s'$으로 이동할 때, $Q_1(s,a)$를 update하기 위해, $Q_1(s',a')$가 최대가 되는 action $a'$을 $Q_2$에서의 action-value를 통해 update함을 알 수 있다. 이를 Sudo-Code로 나타내면 아래와 같다.

해당 논문에서 Q-Learning보다 Double Q-Learning의 Q가 더 낮아 Maximization Bias Problem을 해결할 수 있음이 증명되었다.
'Reinforcement Learning' 카테고리의 다른 글
| Model-based RL (1) | 2024.01.28 |
|---|---|
| n-Step Bootstrapping (1) | 2024.01.22 |
| State-Action-Reward-State-Action (0) | 2024.01.20 |
| Temporal Difference Method (0) | 2024.01.19 |
| Monte Carlo Method (0) | 2024.01.19 |




