| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- GIT
- 백준
- MySQL
- YoLO
- NLP
- 딥러닝
- opencv
- UC Berkeley
- dfs
- RL
- DP
- image processing
- 머신러닝
- deep learning
- dynamic programming
- AlexNet
- Reinforcement Learning
- Python
- hm3dsem
- BFS
- 그래프 이론
- CS285
- machine learning
- C++
- r-cnn
- 강화학습
- LSTM
- hm3d
- ubuntu
- CNN
- Today
- Total
JINWOOJUNG
[ 영상 처리 ] Ch1. Fundamentals 본문
본 영상 처리 개념과 기법들에 대한 공부를 진행하면서 배운 내용들을 중심으로 정리한 포스팅입니다.
책은 Computer Vision: Algorithms and Applications를 기반으로 공부하였습니다.
또한, 인하대학교 박인규 교수님의 디지털 영상 처리 과목을 기반으로 제작된 포스팅입니다.
Image Processing
영상 처리를 위한 Image Processing은 아래의 Step으로 구분된다.
- Image Digitization
- 연속적인 밝기 값을 픽셀 공간에서의 discrete(별개의)한 값으로 변환하는 과정 즉, 이미지를 티지털화 하는 과정이다.
- Sampling - spatial discretization
- 말 그대로 샘플링 과정이다. 특정한 픽셀공간(단위)로 구분하여, 특정 공간에 다수의 값이 있다면 하나의 대표 값으로 설정하는 과정이다.
- Over-Sampling : 추가적인 시간과 많은 메모리 공간이 요구됨
- Under-Sampling : Aliasing 발생 가능
- Quantization
- 연속적인 빛의 Intensity(강도)를 discrete한 Gray Level로 변환하는 과정이다. 즉 Sampling을 통해 구분되어진 한 공간의 픽셀의 값을 0~255의 Digital Value로 변환하는 과정이다.

연속적인 토끼 이미지에서 Sampling 과정을 통해 각 픽셀에 해당하는 값들을 저장하여 디지털화 한다. 하지만 이때의 값은 아날로그 값이기 때문에 Quantization을 통해 Digital Value로 변환한다.
Digital Image Fundamentals
다양한 영상 처리의 용도를 살펴보자
Structure of Human Eye
실제로 사람의 눈에서 일어나는 인식 과정은 Fovea(중심와)에 빛이 들어와 초점이 맺힘으로써 진행된다. 이때, 색상을 인식하는 세포는 크게 원추 세포(Cone Cell)와 간상 세포(Road Cell)로 구분된다.


원추 세포는 장파장(Red), 중파장(Green), 단파장(Blue)에 반응하는 3가지 종류로 구성되어 있으며, 실제 상이 맺히는 Fovea에 많이 분포한다.
간상 세포는 어두운 곳에서 동작하는 세포이다.
Brightness Discrimination(밝기 구분) - Weber ratio $\Delta I_c / I$
- Weber ratio는 밝기 변화를 감지하기 위한 Value
- 어두운 곳에서는 밝기 차이가 커야 다른 밝기라고 느끼지만, 밝은 곳에서는 밝기 차이가 조금만 나도 다른 밝기라고 느낄 수 있다.
위 수식에서 $I$는 Background Illumination(조명, 빛)을 의미한다.

위 그래프를 보면 $I$가 줄어들수록 즉, 어두울수록 Weber ratio가 커지기에 그만큼 밝기 변화량이 더 많이 요구된다.
Psychovisual Effects(심리적 시각효과)

인지되는 빛의 Intensity는 경계 부분에서 Undershoot 혹은 Overshoot가 발생함을 알 수 있다. 이러한 경계 부분을 Mach band pattern이라 하며, 두 개의 인접한 영역의 밝기나 색상 차이를 과장해서 인식하게 된다.

위 사진에서 주변 배경에 따른 상대적 밝기 인식을 알 수 있는데, 첫번째 사진보다 마지막 사진의 사각형이 더 어둡게 보인다. 이는 주변 인접한 영역의 색상 차이가 마지막이 더 크기 때문이다. 이를 Psychovisual Effects라 한다.
Lens
렌즈는 빛은 모으거나 퍼뜨리는 역할을 한다. 특히, 카메라에서는 빛을 모아주는 렌즈의 기능을 사용한다. 렌즈를 살펴보기 전에 기본적인 카메라 모델인 핀 홀 카메라 부터 살펴보자.
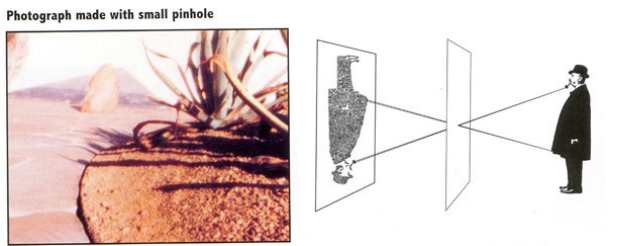

핀 홀 카메라 모델은 왼쪽 사진과 같이 빛이 하나의 구멍을 통해 들어와 반대편에 도립 상이 맺히는 모델이다. 렌즈 모델은 오른쪽 사진과 같이 렌즈를 통해 들어온 빛이 반대편에 도립 상을 만드는 모델이다. 두 모델에 차이는 빛의 양에서 발생하는데, 렌즈 모델이 상대적으로 더 많은 빛을 모을 수 있기 때문에 더 밝은(명확한) 상이 맺힘을 확인할 수 있다. 따라서 만약, Image Plane이 앞으로 오게 된다면 한 점에 대한 빛이 분산되어 흐릿해 질 수 있다(초점의 변화가 발생).
따라서 실제로는 렌즈 모델을 사용하지만, 기하학적 모델이 더 간단한 핀 홀 모델을 이용하여 기하학적 투영 모델을 분석하곤 하는데 둘 사이에는 큰 차이가 없음을 뒤에서 알 수 있을 것이다.
렌즈 모델을 자세히 살펴보면 다음과 같다.


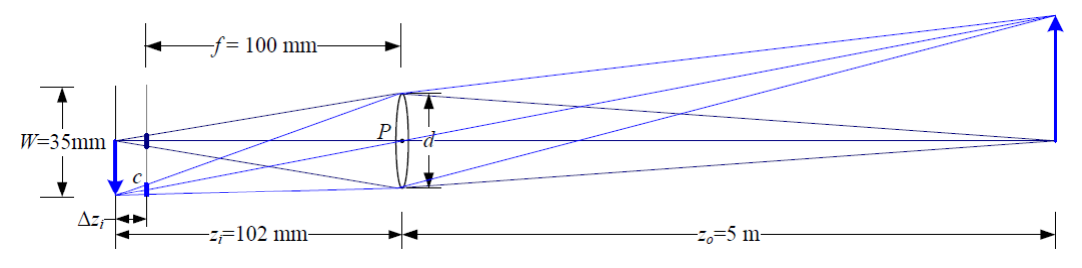
해당 수식에서 $f$는 초점 거리, $z_i$는 상이 맺히는 지점, $z_o$는 물체와의 거리를 의미한다. 즉, $z_o, f$를 알고 있다면 $z_i$를 계산할 수 있다. 핀 홀 모델에서는 $f=z_i$이고, 렌즈 모델에서는 수식에 근거하여 동일하게 만들 수 있으므로 렌즈 모델 대신 핀 홀 모델을 사용해도 무방함을 알 수 있다.
Depth of Field(심도)
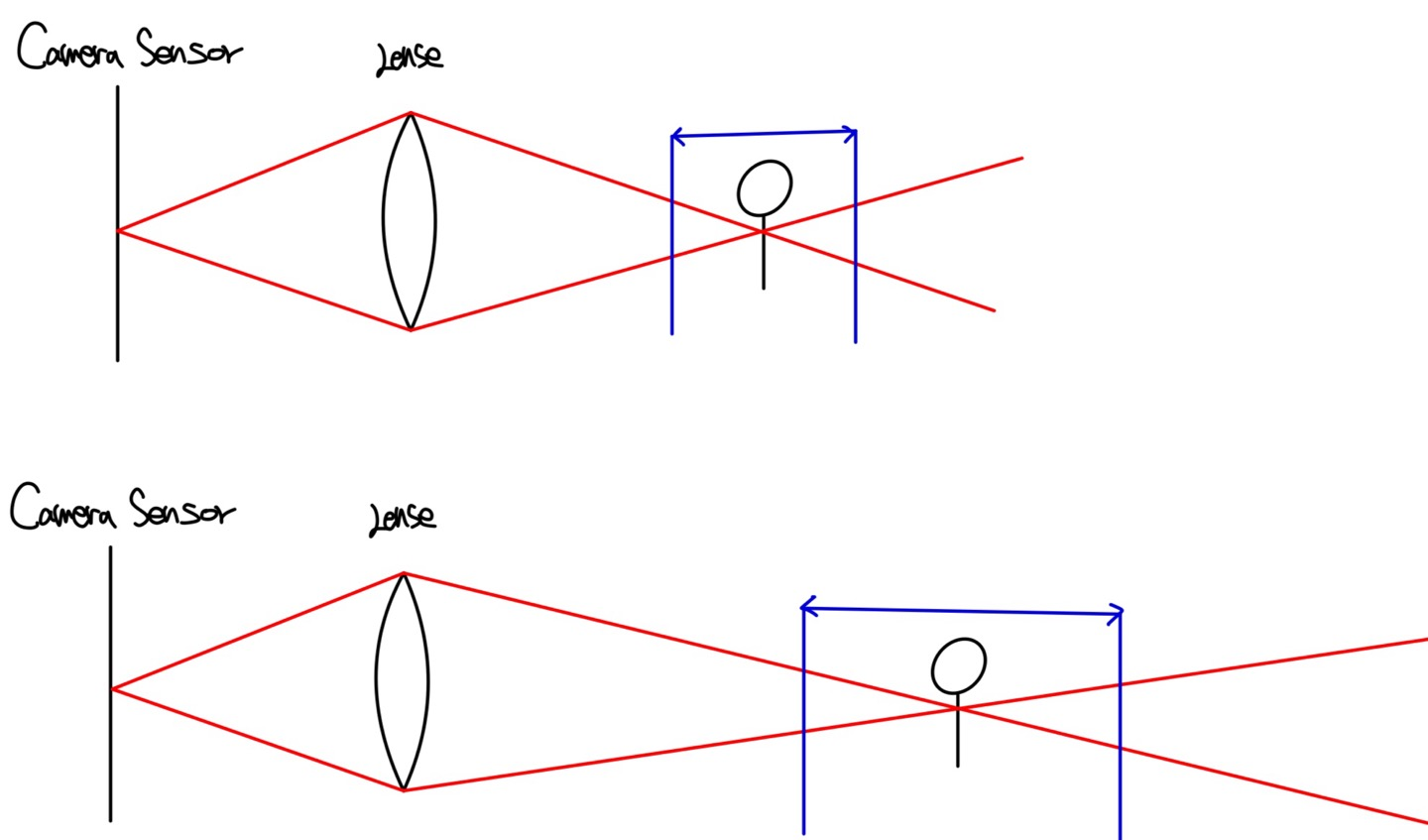
심도는 보라색으로 표현되는 조리개에 따라 달라진다.

상단의 그림은 주변환경이 블러처리가 되는 아웃포커싱이 됨을 알 수 있다. 즉, 조리개가 많이 열리면 심도가 얕아져(작아져) 초점이 맞는 길이가 짧아진다. 초록색으로 표현되는 영역이 심도인데, 심도안에 객체가 존재하면 초점이 맞게 찍힌다. 즉 심도가 얕으면 멀리 있는 객체는 초점이 어긋나 블러 처리가 된다. 반대로 조리개가 적게 열리게 되면 심도가 깊어(커)져 초점이 덜 흐려지게 되어 배경과 객체 모두 정확하게 촬영된다.
심도를 조절하는 방법은 다양하다.
- f 값이 크다 = 조리개 구경이 작다 = 심도가 깊다
- 초점거리가 짧다 = 조리개 구경이 크다 = 심도가 얕다
- 이는 동일한 조리개 값을 기준으로 한다.
- 대상과의 거리가 멀다 = 빛이 퍼지기 시작하는 각도가 작다 = 심도가 깊다
Field of View(FOV : 화각)
화각은 초점거리에 따라 변화하는데, 초점거리가 짧을수록 광각이 되고, 초점거리가 길수록 망원이 된다.
즉, 같은 피사체에 대하여 초점거리가 긴 망원렌즈일수록 크고 좁은 범위가, 초점거리가 작은 광각렌즈일수록 작고 넓은 범위가 촬영된다.


Exposure(노출)
노출은 말 그대로 빛을 얼마나 많이 받아 들였냐 즉, 빛에 노출된 정도를 의미한다. 노출정도를 조절하는 방법은 크게 두가지가 있다.
- Shutter Speed : 빛에 노출되는 시간 조절
- Blur가 발생하는 상황 : Shutter Speed가 길어 대상의 움직임이 모두 관측되는 Motion Blur
- Aperture : 한번에 빛을 받아들이는 양
- Blur가 발생하는 상황 : De-Focus(아웃포커싱)
Shutter Speed
Shutter Speed는 센서를 빛에 노출하는 시간이다. Shutter Speed가 클수록 노출 시간이 길어져 빛을 많이 받을 수 있다. 이는 내가 찍고자 하는 상황에 따라 다른데, 만약 움직이는 물체의 순간적인 움직임을 포착하고 싶다면 Shutter Speed를 낮춰 순간적인 모습을 포착할 수 있다. 하지만 동일한 상황에 대하여 Shutter Speed를 늘리면 잔상이 남는다.

Aperture(조리개)
조리개는 한번에 들어오는 빛의 양을 조절한다.

조리개가 열려있는 구멍의 넓이는 위 식으로 계산되는데, 이때 $\frac{f}{N}$ 은 조리개의 직경을 의미한다.
조리개가 열린정도를 표현하는 수치는 조리개의 직경으로 표현되고, 이때 f-Number(f값)은 $N$을 의미한다.
따라서 f 값이 작을수록 조리개의 열린 정도가 커짐을 의미한다. 심도를 공부할 때, 조리개의 구경이 클수록 심도가 얕다 즉, f 값이 작을수록 심도가 얕음을 자연스럽게 유도할 수 있다.

f값은 아래 사진과 같이 규격화가 되어 있다. f 값은 $\sqrt{2}$배씩 커지기 때문에 결국 f 값이 커질수록 조리개의 열린 넓이는 2배씩 작아짐을 알 수 있다.

Reciprocity(효혜, 상반성)
위에서 설명한 것 처럼 노출값을 결정하는 파라미터는 Aperture과 Shutter Speed가 존재한다.
Shutter Speed를 낮추면 빛의 양은 덜 받고 순간적인 움직임을 포착 가능하다. 동시에, f 값을 낮춰서 Aperture를 키우면
아웃 포커싱 효과가 생기지만 받는 빛의 양은 증가한다.
반면, Shutter Speed를 높이면 빛의 양을 많이 받지만 움직이는 객체에 대하여 잔상이 생긴다. 동시에, f 값을 키워 Aperture를 낮추면 심도가 깊어지지만, 받는 빛의 양은 감소한다.
동일한 상황에서 Shutter Speed, Aperture를 조절하면 서로 다른 이미지를 얻을 수 있지만, 전체적인 Exposure 양은 수치적으로 조절을 하면 같게 만들 수 있다. 따라서, 내가 찍고자 하는 상황은 동일한 Exposure에 대하여 서로 다른 이미지 결과를 얻을 수 있다는 의미이다. 동일한 빛의 양에 따른 Shutter Speed 와 Aperture의 조합은 아래와 같다.

이에 따른 동일한 장면에 대한 촬영 결과는 아래와 같다.

왼쪽은 Shutter Speed가 길어 잔상이 생기지만, Aperture가 낮아 심도가 깊음을 알 수 있다. 하지만 오른쪽 사진은 Shutter Speed가 짧아 순간적인 움직임이 포착 되었지만, Aperture가 높아 심도가 얕음을 알 수 있다.
Sensitivity(ISO) : 감도 - 국제 표준 기구
빛은 카메라의 CMOS Sensor를 통해 전압으로 변환된다. 이는 전기적인 신호이기 때문에 증폭 가능하다.
이때, ISO는 전기적인 증폭량을 의미하며, ISO가 커질수록 받아온 빛을 증폭시켜 더 많이 받아오지만, 그만큼 Noise가 발생하게 된다.
따라서 빛의 양이 적은 어두운 상황에서 Shutter Speed를 줄이고, ISO를 높여 야간 촬영을 하지만 그만큼 Noise도 발생하게 된다.

Vegnetting(비네팅)
렌즈의 중심과 가장자리에 통과하는 광량의 차이가 발생하여 바깥쪽의 광량이 더 적기 때문에 어둡게 나오는 현상이다.
가볍게 넘어가자.

Chromatic Aberration(색수차)
색의 파장에 따라 굴절률이 다르기 때문에 빛이 한 점에서 모이지 않아 이미지가 흐릿해 지는 현상이다.
아래 사진에서 보면 파장에 따른 굴절률의 차이가 존재함을 확인할 수 있다. 이는 서로다른 굴절률의 렌즈를 조합함으로써 해결 가능하지만, 가볍게 넘어가자.



Digital Image
디지털 이미지는 아래와 같은 구조로 존재한다. 좌측 상단이 (0,0)이고 오른쪽으로 x의 양의 방향, 아래족으로 y의 양의 방향인 픽셀 단위로 구성되며, 각 픽셀의 값(Pixel Intensity)은 0~255의 Descrete Value이다.

위 이미지는 520 x 500의 픽셀로 구성되어있으며, 이는 해당 이미지의 해상도를 결정하게 된다.
Image Resolution(해상도)
해상도는 앞서 언급한 것 처럼 픽셀의 수로 결정된다(Width x Height). 이는 공간 해상도(Spatial Resolution)로, 이미지가 몇개의 픽셀로 구성되어 있는지를 의미한다.
반면, Intensity Resolution은 한 픽셀의 밝기 값이 몇 비트로 표현되는지를 의미한다. 표현 비트가 더 많을수록, 한 픽셀에 대하여 더 세분화된 밝기 표현이 가능하며, 0~255의 범위로 표현되는 일반적인 밝기는 $2^8$으로 총 256개의 밝기를 표현할 수 있다.
Uniform Sampling
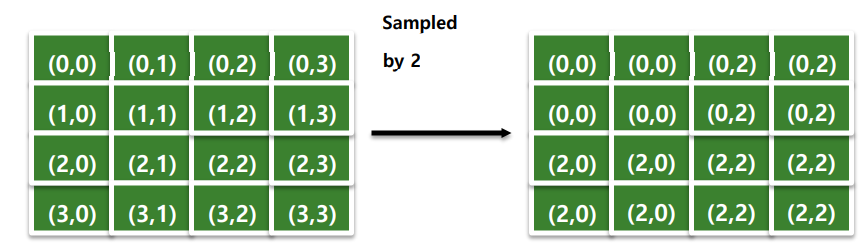
위 과정처럼 Down Sampling을 진행한다고 생각 해 보자. 왼쪽의 Original Image로 부터 Sampled by 2가 진행되면, 4개의 픽셀에 대하여 젤 왼쪽 위의 값이 나머지의 픽셀의 값을 대표한다고 생각하면 된다. 하지만 지나친 Down Sampling은 몇가지 문재를 야기할 수 있다.
Aliasing(에일리어싱)
Aliasing은 Sampling 과정에서 원본을 정상적으로 복원하지 못하고 일그러지는 즉, 신호의 왜곡이 발생하는 것이다.

원본 신호가 있고 이를 적절하게 샘플링 한다면 위 그림처럼 원보 신호를 정상적으로 복원할 수 있다. 하지만 샘플링 주기가 길어 낮은 샘플링이 진행된다면 원본 신호를 정상적으로 복원하지 못한다.
이와 관련하여 Nyquist Theorem(나이퀴스트 이론)이 존재하는데, "샘플링하려는 원신호의 주파수보다 2배 이상의 빠르기로 샘플링을 해야 정확한 신호를 복원할 수 있다"고 한다. 즉, 원래 신호보다 더 빠른 고주파 신호로 샘플링을 해야지 원 신호를 복원할 수 있다는 의미이다.

왼쪽 오른쪽 이미지를 Sampled by 2를 한 결과이다. 바지쪽의 줄무늬를 보면 원본 이미지를 정상적으로 표현하지 못함을 알 수 있다. 줄무늬는 일종의 고주파 성질을 갖기 때문에 그곳을 다운 샘플링 한 결과 Aliasing이 발생함을 알 수 있다.
조금 다르게 표현하자면, 바지 줄무늬 같은 미세한 패턴을 더 큰 픽셀 그리드에 맞게 Down Sampling 되기 때문에 Aliasing이 발생한다고 생각하면 더 쉬울 것이다. 이러한 패턴을 Moire Pattern이라 한다.
Uniform Quantization
해상도를 설명하면서 한 픽셀의 Intensity를 0~255 즉, 8비트 표현한다고 하였다. Quantization은 결국 한 픽셀의 밝기 표현을 의미하며, 표현 가능한 비트수가 많을수록 더 세분화된 밝기 표현이 가능하다.
하지만, 비트 수가 감소한다면 부드러운 밝기 변화가 끊겨 보이는 현상이 발견된다.

Color Sensing
빛은 Sensor를 통해 광량으로 빛의 Intensity 정보를 가져온다. 이때, 각 칼라 필터는 특정한 색의 Intensity를 추출하는데, 이러한 격자 형태를 Bayer Grid(Pattern)이라 한다. 각 필터는 실제로 우리가 잘 아는 R,G,B의 색을 추출함을 알 수 있다.

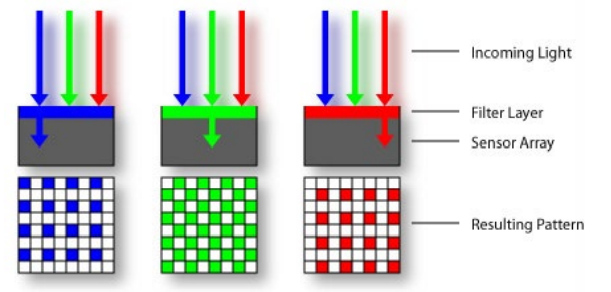
하지만, 각 Grid의 필터는 특정한 한 색의 Intensity 밖에 받아들이지 못한다. 하지만 하나의 색상을 결정하는 요소는 R,G,B로 이루어져 있다. 따라서 주변의 RGB Value를 이용해 평균값으로 자신의 RGB을 추정하는 것을 Demosaicing이라 한다.

'2024 > Study' 카테고리의 다른 글
| [ 영상 처리 ] Part2-1. OpenCV Mask Processing(C++) (0) | 2024.04.07 |
|---|---|
| [ 영상 처리 ] Part1-2. OpenCV Image Processing(C++) (0) | 2024.04.06 |
| [ 영상 처리 ] Part1-1. OpenCV Image Processing(C++) (0) | 2024.04.06 |
| [ 영상 처리 ] Ch2. Point(Pixel) Processing (0) | 2024.04.03 |
| [ 영상 처리 ] OpenCV 환경설정(Window, Visual Studio) (0) | 2024.03.03 |




