| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 딥러닝
- 머신러닝
- UC Berkeley
- LSTM
- 백준
- YoLO
- hm3dsem
- 강화학습
- r-cnn
- C++
- dfs
- NLP
- machine learning
- deep learning
- ubuntu
- hm3d
- BFS
- DP
- opencv
- CNN
- AlexNet
- RL
- Python
- GIT
- CS285
- Reinforcement Learning
- 그래프 이론
- image processing
- MySQL
- dynamic programming
- Today
- Total
JINWOOJUNG
[ 영상 처리 ] Ch2. Point(Pixel) Processing 본문
본 영상 처리 개념과 기법들에 대한 공부를 진행하면서 배운 내용들을 중심으로 정리한 포스팅입니다.
책은 Computer Vision: Algorithms and Applications를 기반으로 공부하였습니다.
또한, 인하대학교 박인규 교수님의 디지털 영상 처리 과목을 기반으로 제작된 포스팅입니다.
Before This Episode
https://jinwoo-jung.tistory.com/49
[ 영상 처리 ] Ch1. Fundamentals
본 영상 처리 개념과 기법들에 대한 공부를 진행하면서 배운 내용들을 중심으로 정리한 포스팅입니다. 책은 Computer Vision: Algorithms and Applications를 기반으로 공부하였습니다. Image Processing 영상 처
jinwoo-jung.tistory.com
Point(Pixel) Processing
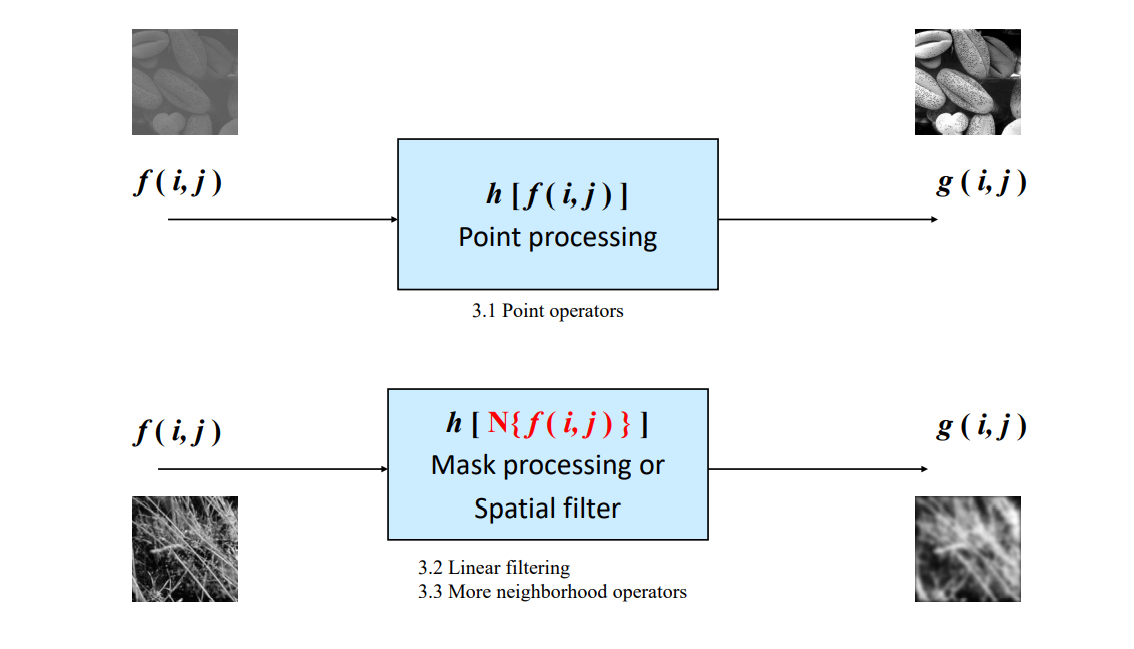
Image Processing의 기법 중 Point Processing과 Mask Processing(Spatial Filter)이 있다.
$f(i,j)$를 픽셀 좌표 $(i,j)$에서의 밝기 라고 하면 두 기법의 차이는 다음과 같다.
- Point Processing
- 독립적인 Pixel 하나하나 연산을 통하여 영상 처리
- Ex) 각 픽셀의 밝기 값이 어두우면 더 어둡고, 밝으면 더 밝게 처리하여 이미지를 대조시킴
- Mask Processing(Spatial Filter)
- Pixel 하나하나가 아닌 하나의 Pixel을 처리하는데 인접한 Pixel의 밝기값도 고려
- Ex) 특정 Pixel을 Blur처리 하기 위해 주변 Pixel의 화소값도 고려
Point(Pixel) Processing
Image Negative(음화)

이미지의 양과 음을 바꾸는 영상 처리 기법. 위 사진처럼 오른쪽 사진이 사람이 인식하기에 더 대조가 잘 됨을 확인 가능.
Log Transformation(Dynamic Range Compression)

화소 밝기에 로그를 씌워 로그 스케일을 적용하는 영상 처리 기법.
왼쪽 사진을 보면 Maximum Value만 가운데에 매우 크고, 나머지 부분은 매우 작은 범위 내에서 Pixel Value를 가짐을 알 수 있다. 즉 어두운 값에서도 차이가 존재하지만, Maximum Value가 상대적으로 매우 크기 때문에 밝은 값과 대비되어 잘 보이지 않는다.

위와 같이 $S = \frac {r}{1+r}$의 방정식이나 Log Function을 사용하여 Pixel Value를 Pre-Processing 해 준다면, 큰 값과 작은 값의 차이를 완화시켜 작은 Value를 펼쳐주기 때문에 오른쪽과 같이 차이가 어두운 값 내에서도 차이가 명확히 보인다.
Histogram Equalization

히스토그램을 평탄화 시키는 영상 처리 방법으로, 이미지의 대조를 더 명확히 표현하기 위한 방법이다. 원본 이미지는 전체적인 픽셀값의 분포가 60~170 사이에 분포함을 히스토그램을 통해 알 수 있다. Histogram Equalization을 통해 해당 픽셀 분포 범위를 0~255 전체적인 범위로 평탄화시켜 넓힘으로써 대조효과가 더 명확해 짐을 확인할 수 있다.
Gamma Correction
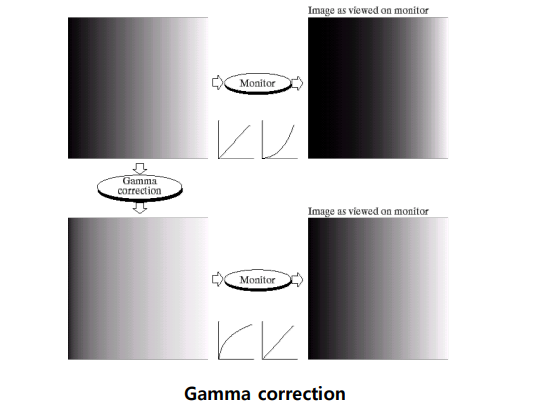

화소 밝기를 지수 함수로 바꾸는 영상 처리 방법으로, 하드웨어적인 문제로 영상에서 나오는 밝기 값이 실제와 차이가 발생하는데, 이를 실제와 동일하게 보정하는 영상 처리 방법이다.
실제 영상 밝기를 왼쪽 상단 처럼 선형적이라고 하자. 하지만 모니터는 오른쪽 상단처럼 비선형적으로 밝기가 증가하고 우리는 이를 알고 있다. 따라서 모니터 밝기와 반대로 비선형적으로 증가하는 Input(지수 함수)을 줌으로써 최종 Output이 선형적으로 되도록 하는 방법이다. 해당 지수함수는 하드웨어적인 환경에 따라 $\gamma$값을 변형시켜 적용하면 된다.
Contrast Stretching
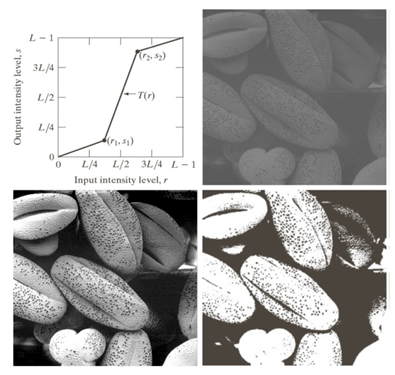
Constrast Stretching은 이미지에서 특정 부분의 밝기 대비 효과를 극대화 시키는 방법 중 하나이다. 오른쪽 상단 그래프는 픽셀 Value를 변형시키는 Transformation Function 인데, $T(r)$부분은 기울기가 보다 커 해당 범위의 Intensity(밝기값)이 증가하고, 나머지는 기울기가 1보다 작아 Intensity가 압축됨을 알 수 있다.
Constrast Stretching의 필요성은 아래 두 그림에서 알 수 있다. 우측 상단 원본 이미지에 대하여 Constrast Stretching 결과는 왼쪽 하단과 같고, Thresholding 결과는 오른쪽 하단과 같다. Thresholding은 특정 임계치를 넘게 되면 255 아니면 0으로 설정한다(flag에 따라 다름). 따라서 원본 이미지를 유지하기 보다는, 극단적인 대조 효과를 보인다. 하지만 Constrast Stretching 결과 대조효과를 더 극대화 하면서 원본 이미지를 유지함을 알 수 있다.
Gray-Level Slicing
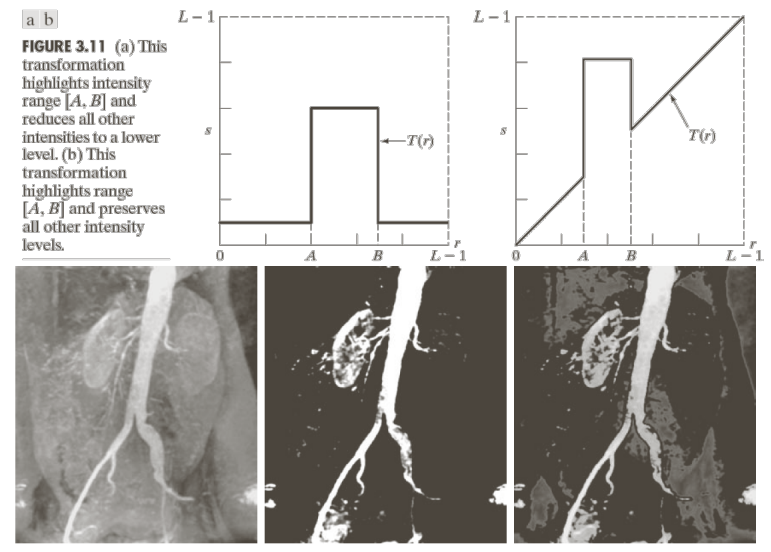
특정한 Pixel Value 영역을 기준으로 밝기값을 조절하는 영상 처리 기법이다.
첫번째 그래프는 $A,B$를 제외한 모든 영역의 밝기 값을 0에 가까운 값으로 설정함을 알 수 있다.
반면, 두번째 그래프는 $A,B$를 제외한 모든 영역의 밝기는 유지하면서, 해당 영역은 원본보다 더 밝은 값으로 설정함을 알 수 있다.
우리가 추출하기 원하는 영역, 대상의 밝기 값 분포를 알고 있다면, 해당 영역 제외 모두 0으로 설정하여 원하는 영역만 확인할 수 있다.
Bit-Plane Slicing
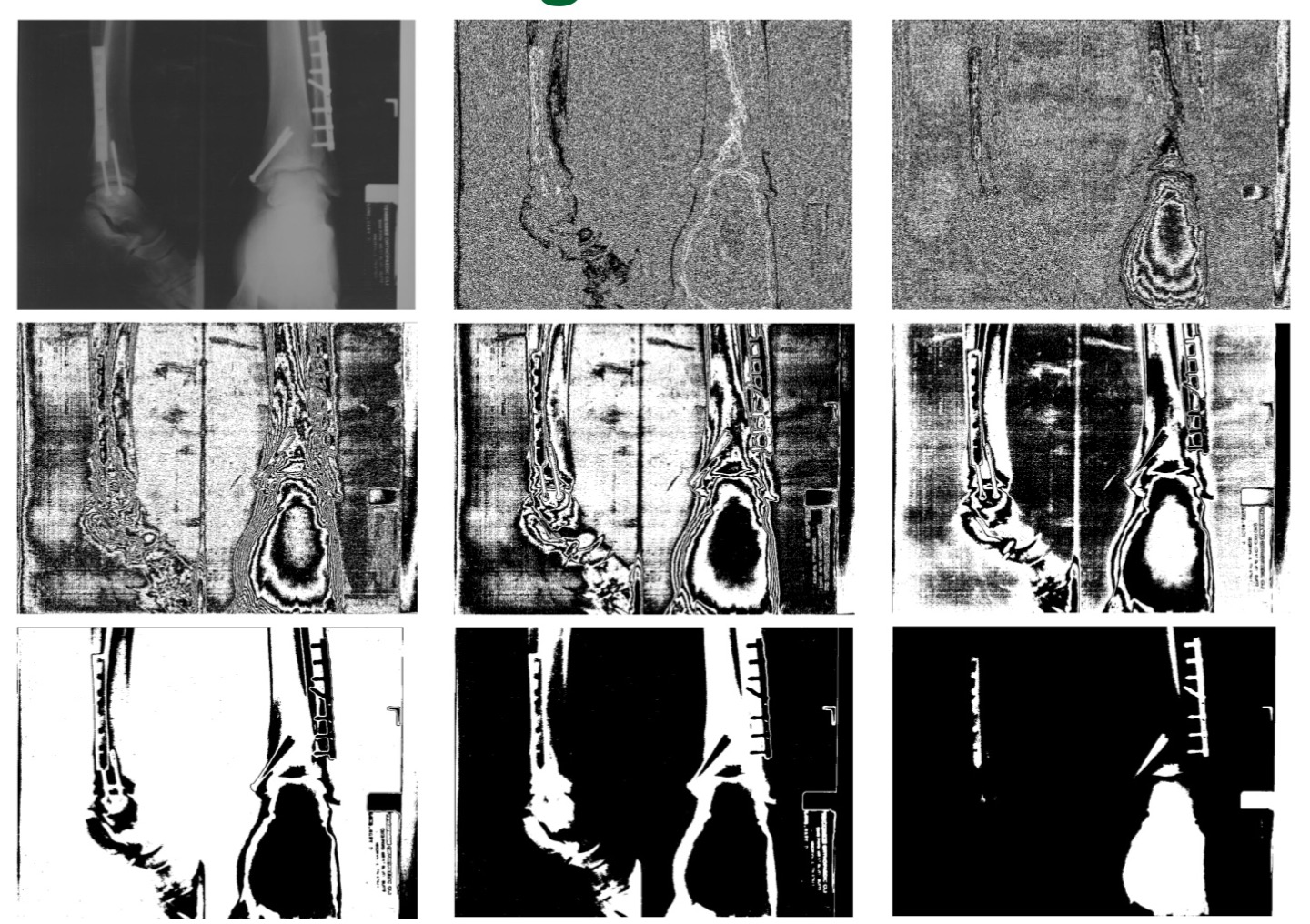
Bit-Plane Slicing은 이미지의 각 픽셀 값을 이진수로 표현했을 때의 각 비트 수준(Plane)을 분리하여 분석하거나 처리하는 영상 처리 방법이다.
이전에 Grayscale Pixel Value는 0~255의 범위를 가지는 8bits이다. 따라서 한 픽셀의 픽셀값은 8개의 2진수로 나타낼 수 있다. 따라서 전체 이미지에 대하여 각 픽셀을 비트 수준(Plane)에 대하여 0,1인지 구분하고, 1이라면 해당 Plane에 255를 나타내고 0이라면 0을 나타내는 방법이다.
$2^7$을 나타내는 비트 Plane을 보자. 255에 가까운 즉, 흰색에 가까울수록 해당 픽셀 값은 128을 넘길 것이다. 따라서 해당 비트 자리에는 1이다. 하지만 어두운 값은 해당 비트자리에는 0이 들어갈 것이다. 이처럼 극단적인 색상 비교를 하거나, 각 비트 수준으로 분리하여 처리할 때 이와 같은 방식을 사용한다.
이전까지 살펴본 Pixel Processing은 픽셀 분포도를 기반으로 어떤 방법을 적용할지 결정된다. 이때 기본적으로 사용되는 것이 Histogram 이다.
Histogram
Histogram은 특정 Intensity를 갖는 Pixel의 분포도를 그래프로 나타낸 것이다.


기본적인 수식은 설명한 것과 같이 각 Intensity에 해당하는 화소의 개수를 계산한다고 생각하면 된다.
이때, $n_k$는 특정 Intensity $k$의 Histogram으로, 몇개의 픽셀이 $k$의 Intensity를 갖는지를 나타낸다. 이를 전체 픽셀 개수인 $N$으로 나눠주면 결국 특정 Intensity $k$를 가질 확률이 된다. 이를 Normalized Histogram이라 한다.
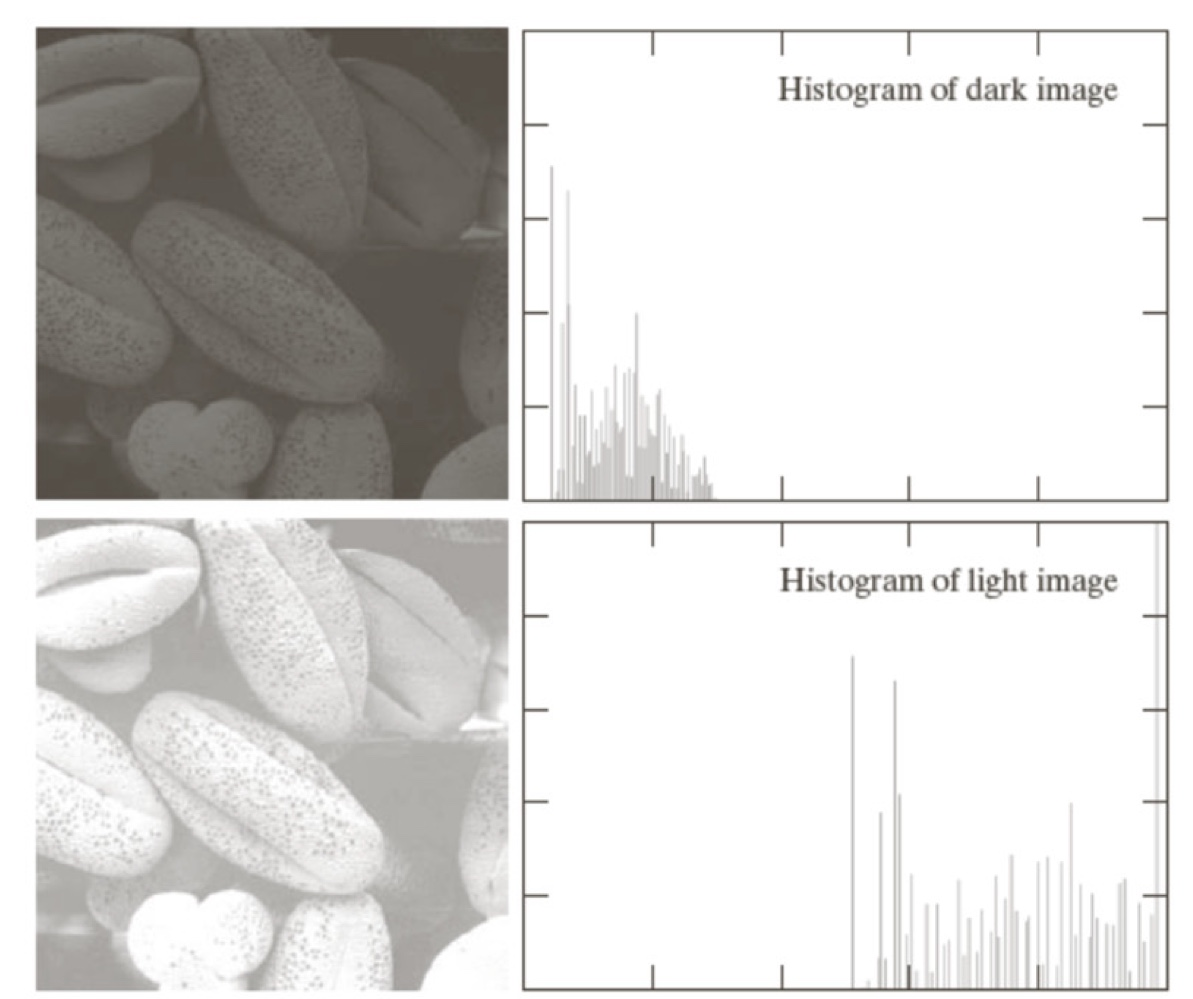

오른쪽 아래 이미지를 제외하고 나머지는 모두 특정 범위 내에 Intensity가 몰려 있음을 알 수 있다. 특히, 오른쪽 상단 이미지를 보면 몰려있는 구간이 매우 작다. 따라서 각 픽셀 간의 대비가 거의 없음을 확인할 수 있다. 하지만 오른쪽 아래 이미지의 경우 Intensity 분포가 0~255 전체 범위에 대해 골고루 분포함을 알 수 있다. 따라서 대비가 확실한데, 이처럼 특정 범위에 몰려있는 이미지를 고루고 분포된 히스토그램을 갖도록 하는 Pixel Processing을 진행하는데, 이를 Histogram Equalization이라 한다.
Histogram Equalization

앞서 언급한 것처럼, Histogram Equalization은 특정 구간에 몰린 Intensity를 고루게 분포될 수 있도록 평활화 시키는 방법이다.
이전에 Histogram Equalization과 유사한 Histogram Stretch에 대해서 잠깐 언급하고 넘어가자. Histogram Stretch도 평탄화를 하는 방법 중 하나이다. 하지만 이전의 분포 비율을 그대로 유지한 체 전체 범위를 0~255로 늘리는 방법이다. 따라서 Stretch 적용 이전에 분포하는 형태는 유지된 채(Peack 점) 전체 범위로 확장된다고 생각하면 된다.

Histogram Equalization을 통해 Intensity의 분포를 퍼뜨리게 되면 오른쪽과 같이 분포가 넓어지고 대비효과가 더 명확해 짐을 알 수 있다. 하지만, 분포는 전체적으로 퍼졌지만 아직 "평활화"가 되었다기엔 부족한 모습을 보인다. 조금 더 효과적인 평활화 방법이 없을까?
Histogram Equalization - Derivation
Histogram을 설명하면서 Normalization을 진행하면 그것은 특정한 Intensity $k$를 가질 확률이 된다고 하였다.
따라서 Hitogram은 결국 0~255 중에서 특정한 값을 가지는 확률 변수이다.


$S$를 우리가 원하는 평평한 확률 분포를 가지는 확률 변수라고 하자. $T$는 Transformation Function으로 기존의 $r$의 확률 분포를 가지는 확률 변수를 $T$를 통해 평평하게 한다고 하자.
$p_s(s)$는 확률변수 $s$의 확률 밀도 함수를 의미하는데, 오른쪽 식은 결국 확률 변수의 변환에 의한 확률 밀도 함수의 변환 공식이다. 위 식을 아래와 같이 쓸 수 있는데,
$$ds p_s(s) = dr p_r(r)$$
$s=T(r)$에 의해서 미소 구간에서의 $s$와 $r$의 확률 자체는 같아야 한다(둘은 연관관계를 가짐). 따라서 $ds p_s(s)$ 즉, 확률 밀도 $p_s(s)$를 가지는 미소 구간 $s$에서의 확률은 $dr p_r(r)$ 즉, 확률 밀도 $p_r(r)$를 가지는 미소 구간 $r$에서의 확률과 같게 된다.
이를 다시 정리하면 오른쪽의 식이 되는데 이는 원래 확률 변수의 확률 밀도 함수를 미분한 것으로 나누면 새로운 확률 변수의 확률 밀도 함수가 됨을 의미한다. 우리는 새로운 확률 밀도가 평평하게 즉 1이 되길 원한다.

왼쪽의 그래프는 확률 변수 $r$의 확률 밀도 함수(PDF)이다. 확률 분포 함수는 확률 변수가 확률 변수의 분포를 의미한다. Histogram은 결국 특정 픽셀의 Intensity(확률 변수)가 0~255의 범위에서 어느 분포를 가지는지 나타낸다.
우리가 원하는 것은 확률 밀도 함수의 평탄화! 결국 오른쪽 그래프처럼 Histogram이 평평하게 하는 것이 목적이다.
그럼 어떻게 해야 할까?

결국엔 새로운 확률 분포 $p_s(s)$가 1이 되기 위해서는 분모와 분자가 같아야 하기 때문에 $ \frac {ds}{dr} = p_r(r)$이면 된다. 이를 만족시키는 경우를 확인 해 보니 CDF(확률 누적 함수)와 PDF의 관계를 찾을 수 있다.
$$CDF = \int PDF$$
CDF, PDF는 위의 관계를 같기 때문에 CDF가 $T(r)$이 되고, PDF가 $p_r(r)$ 원래의 확률 밀도 함수가 된다면 결국 $p_s(s) = 1$을 만족할 수 있게 된다. 이를 수식적으로 표현하면 다음과 같다.
$$s = T(r) = \int_{0}^{r} p_r(w) dw$$
하지만 위 식은 연속적인 상황에 대한 식이고, Pixel Intensity의 경우 Discrete하기 때문에 식을 변경하면 다음과 같다.
$$s_k = T(r_k) = \sum_{j=0}^{k} \frac{n_j}{n} = \sum_{j=0}^{k} p_r(r_j)$$
정리해보자.
우리는 원래 Histogram(확률 분포)를 가지는 확률 변수 $r$의 확률 밀도 함수를 평평하게 만들기 위해서 Transformation Function으로 확률 누적 함수를 이용할 것이다. 즉, 평활화를 위해 지금까지의 Histogram을 합친다고 보면 된다.


예제를 하나 보자. 간단하게 설정하기 위해 Intensity는 3bit로 표현되고, 이는 0~7 범위를 이룬다. 또
한 전체 픽셀 수는 64*64로, MN = 4096이다. 따라서 $r_k$는 각 픽셀의 Intensity, $n_k$는 각 Intensity에 해당되는 화소 갯수이다.
따라서 히스토그램 즉, $p_r(r_k)$는 단순히 전체 픽셀수에서 해당 Intensity의 픽셀수로 나누면 구할 수 있다. Histogram은 오른쪽과 같다.
이제 CDF를 계산하면 왼쪽 그래프와 같다.
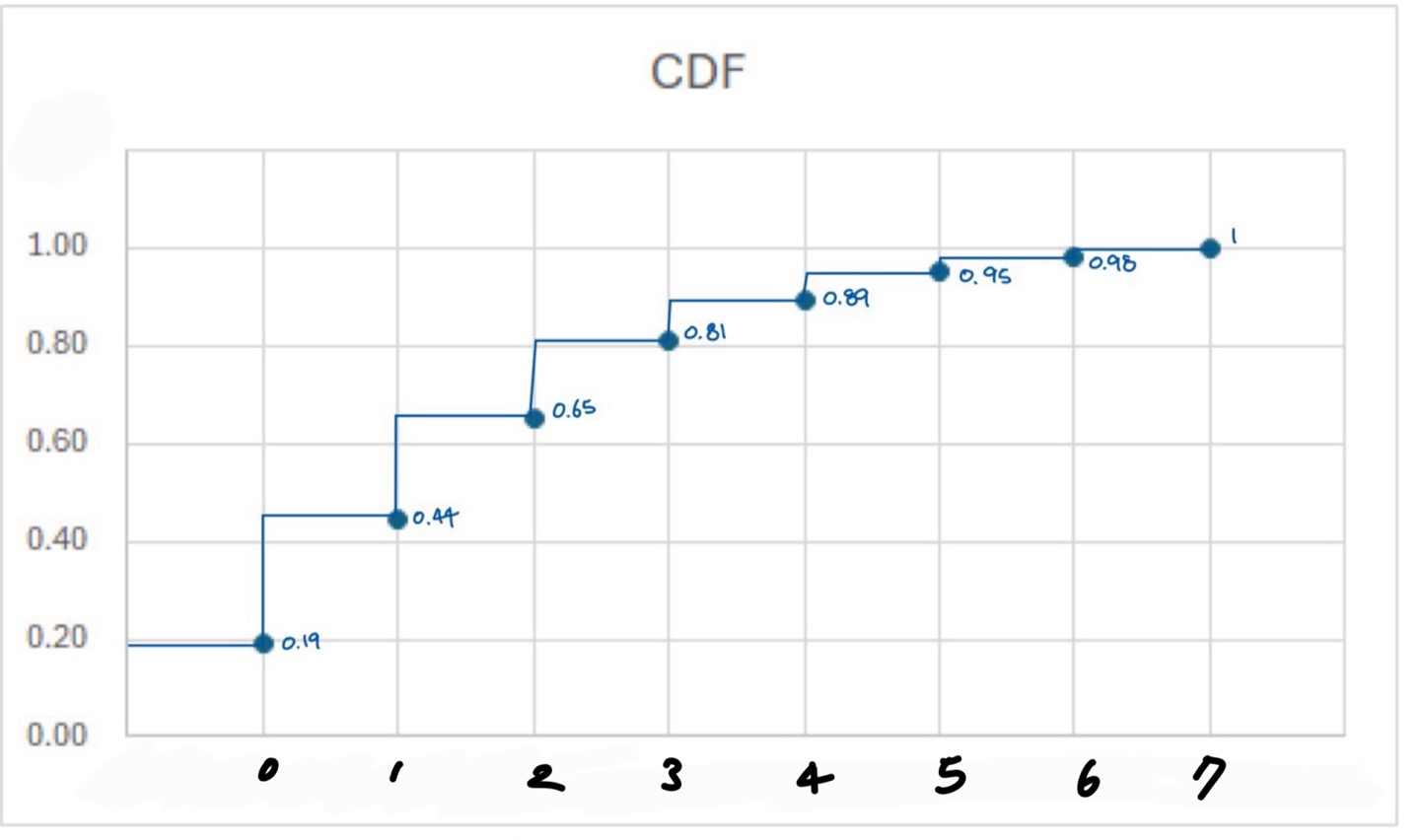
단순히 누적 이기 때문에, $T(r_0) = 0.19, T(r_1) = 0.19+0.25=0.44$, /cdots$이다. 확률이기 때문에 결국 누적합은 1이 된다. 하지만 이를 다시 매핑하여 $s_k$를 구하는 과정에서 누적 확률에 7을 곱하는 것을 확인할 수 있다. 이는 0~1의 누적확률에서 7을 곱해서 0~7의 Intensity를 나타내는 Histogram Domain으로 변환시킬 수 있기 때문이다.
따라서 CDF를 다시 구해보면 다음과 같다.


가운데 그래프를 보면 $s_k$를 의미하는 y축의 범위가 0~7로 Hitogram Domain으로 변환됨을 확인할 수 있다.
따라서 이제 다시 Mapping 해 보자. 각 누적 확률을 $s_k : 0~7$로 매핑해야 한다. 따라서 $s_3, s_4$의 경우 반올림을 하여 모두 6으로 매핑되는 등의 과정을 거치면 오른쪽 그래프 처럼 평활화가 되었음을 확인할 수 있다.
그렇다면 위 과정을 한번 더 해보자. 더 평탄화가 될까?

한번 더 반복하면 더 잘 될 것 같지만, 결국 결과는 동일하다. 2열은 현재 확률, 3열은 누적 확률, 4열은 7을 곱한 결과 5열은 Histogram Domain으로 옮긴 결과, 6열은 최종적으로 Histogram Equalization을 한 결과 각각의 확률 값이다. 결국 동일하다.
Histogram Equalization을 수행하게 된다면 결국 PDF는 Uniform하게 된다. 즉 평활화가 되기 때문에 그에 대한 CDF는 선형적으로 바뀔 수 밖에 없다.

앞서 설명한 것 처럼, 1번 수행 결과 젤 오른쪽 그래프와 같이 해당 확률 변수의 PDF는 1이다. 따라서 누적한 결과(CDF)는 점점 증가하는 선형적으로 변하게 된다(y=x 의 형태와 동일함).
따라서 Histogram Equalization을 한번 더 수행한다고 하여도 CDF는 (y=x)로 Input과 Output이 동일하기 때문에 수행 결과도 동일하다. 실제로 실행 결과 변화가 없음을 알 수 있다.

첫번재 수행과 두번째 수행의 CDF는 다음과 같다. 두번째 수행의 경우 확률 자체가 0인 값이 있어서 다소 선형적이지 않게 보이지만, 가만하고 확인한다면 선형적임을 확인할 수 있다.
'2024 > Study' 카테고리의 다른 글
| [ 영상 처리 ] Part2-1. OpenCV Mask Processing(C++) (0) | 2024.04.07 |
|---|---|
| [ 영상 처리 ] Part1-2. OpenCV Image Processing(C++) (0) | 2024.04.06 |
| [ 영상 처리 ] Part1-1. OpenCV Image Processing(C++) (0) | 2024.04.06 |
| [ 영상 처리 ] Ch1. Fundamentals (0) | 2024.03.30 |
| [ 영상 처리 ] OpenCV 환경설정(Window, Visual Studio) (0) | 2024.03.03 |




