| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- image processing
- BFS
- C++
- ubuntu
- 백준
- 그래프 이론
- machine learning
- 딥러닝
- LSTM
- opencv
- dfs
- Reinforcement Learning
- CS285
- 강화학습
- UC Berkeley
- hm3d
- dynamic programming
- CNN
- Python
- r-cnn
- NLP
- RL
- MySQL
- deep learning
- hm3dsem
- GIT
- YoLO
- AlexNet
- DP
- 머신러닝
- Today
- Total
JINWOOJUNG
[ 정렬 - 24173 ] 알고리즘 수업 - 힙 정렬 1(C++) 본문
문제
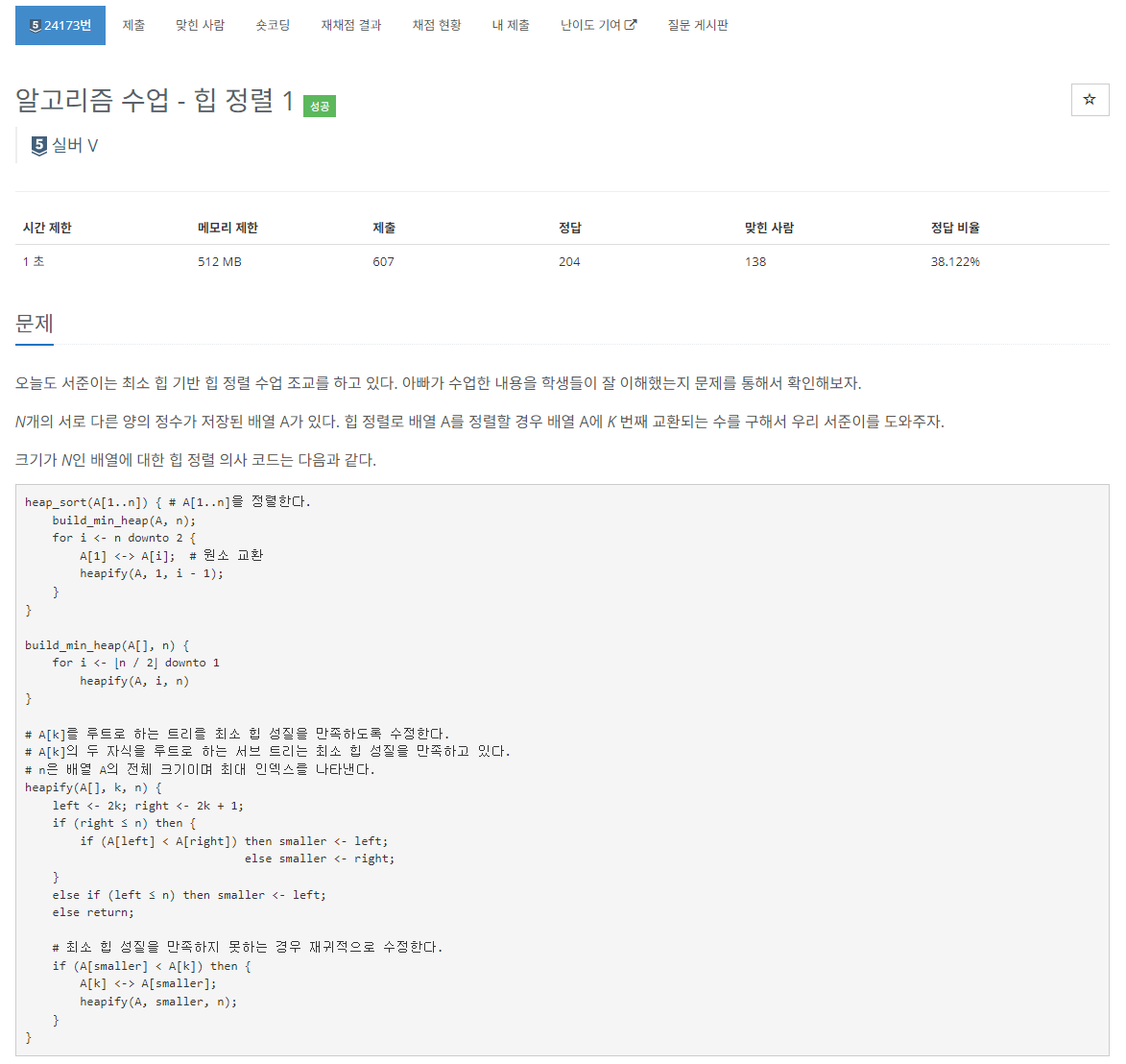

접근법
Heap Sort를 알기 전, Heap에 대해서 알아야 한다.
Heap은 다음과 같은 특징을 가지고 있다.
- Degree = 2
- Complete Binary Tree
- 부모노드와 자식 노드간의 상하관계
- 좌, 우의 상하관계가 아니라 Min, Max Heap에 따른 부모와 자식간의 상하관계
Complete Binary Tree를 조금 더 살펴보면, 노드를 삽입 시 왼쪽부터 즉, 삭제 시 오른쪽 부터 삭제하는 Tree 구조이다.
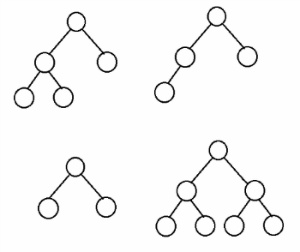
따라서 수도코드를 살펴보면 일반적인 트리 구조와는 다른 모습을 보이고 있음을 확인할 수 있다. Min Heap임을 고려하여 해당 코드를 분석 해보자.
void build_mean_heap(int32_t ars32_A[], int32_t s32_N)
{
int32_t s32_I;
for (s32_I = s32_N / 2; s32_I > 0; s32_I--)
{
heapify(ars32_A, s32_I, s32_N);
}
}
heapsort()에서 가장 먼저 실행되는 코드는 build_mean_heap이다.
현재 입력을 받으면서 해당 노드의 위치가 MinHeap을 고려하면서 삽입 된 상태가 아니기 때문에 전체 노드에 대하여 MinHeap을 만족시키기 위함이다.
이때, heapify를 $s32_N/2$만 하는 이유는 현재 트리구조가 배열로 짜여져 있기 때문에, 부모 노드의 Index가 s32_I이면 자식노드는 2*s32_I, 2*s32_I+1로 접근하기 때문이다.
void heapify(int32_t ars32_A[], int32_t s32_K, int32_t s32_N)
{
int32_t s32_Left = s32_K * 2;
int32_t s32_Right = s32_K * 2 + 1;
int32_t s32_Smaller;
if (s32_Right <= s32_N)
{
if (ars32_A[s32_Left] < ars32_A[s32_Right])
{
s32_Smaller = s32_Left;
}
else
{
s32_Smaller = s32_Right;
}
}
else if (s32_Left <= s32_N)
{
s32_Smaller = s32_Left;
}
else
return;
if (ars32_A[s32_Smaller] < ars32_A[s32_K])
{
int32_t s32_I;
int32_t s32_Tmp = ars32_A[s32_Smaller];
ars32_A[s32_Smaller] = ars32_A[s32_K];
ars32_A[s32_K] = s32_Tmp;
s32_Cnt += 1;
if (s32_Cnt == s32_Kmax)
{
cout << ars32_A[s32_K] << " " << ars32_A[s32_Smaller] << endl;
flag = false;
return;
}
heapify(ars32_A, s32_Smaller, s32_N);
}
}
heapify()는 MinHeap 을 만드는 과정이다.
인자로 들어오는 것은 원본 배열, 탐색할 노드, 배열의 길이(가변)이다.
처음 heapify가 호출되는 build_mean_heap() 내부에서는 전체 배열 길이가 들어온다. 하지만, heapsort() 내부에서 불릴 때에는 해당 값이 점점 주는데 이는 Heap Sort() 과정에서 하나씩 원소를 빼면서 정렬 해 나가지만 해당 기능이 없기 때문에 MinHeap 을 만드는 전체 배열의 길이를 감소 함으로써 정렬하는 범위 자체를 제외시키는 것이다.
먼저 탐색할 노드에서 자식 노들에서 최소값을 찾아낸다. Heap의 경우 부모노드와 자식 노드의 상하관계만을 유지하면 되고, 여기서는 MinHeap 이기 때문에 최소값을 찾아낸다.
만약 부모 노드의 Value가 최소값보다 크면 Swapping이 발생된다. 그리고 다시 heapify(ars32_A, s32_Smaller, s32_N)이 호출되는데, 이때 인자로 s32_Smaller가 들어간다. 즉 swap이후, 원래 부모노드가 자식 노드로 내려가면서 다시 MinHeap 을 만족하는지 확인해야 하기 때문이다.
void heapsort(int32_t ars32_A[], int32_t s32_N)
{
int32_t s32_I;
build_mean_heap(ars32_A, s32_N);
for (s32_I = s32_N; s32_I > 1; s32_I--)
{
if (flag)
{
int32_t s32_Tmp = ars32_A[1];
ars32_A[1] = ars32_A[s32_I];
ars32_A[s32_I] = s32_Tmp;
s32_Cnt += 1;
if (s32_Cnt == s32_Kmax)
{
if (ars32_A[1] < ars32_A[s32_I])
{
cout << ars32_A[1] << " " << ars32_A[s32_I] << endl;
}
else
{
cout << ars32_A[s32_I] << " " << ars32_A[1] << endl;
}
return;
}
heapify(ars32_A, 1, s32_I - 1);
}
else
return;
}
heapsort()는 먼저 전체 트리에 대해서 MinHeap 을 만든다.
이후 for문을 도는데, 이때 Index를 보면 s32_N부터 1씩 감소한다. 처음에 s32_N으로 들어가는 인자는 배열의 전체 길이이다. 즉, Complete Binary Tree를 만족하기 때문에 가장 마지막 노드가 되는 것이다. 따라서 정렬 과정에서 Root원소를 pop()하면서 젤 마지막 원소를 Root로 끌어와서 다시 MinHeap을 유지하는데, 현재 pop() 과정이 없기 때문에 Index 적으로 제한하여 HeapSort()를 진행하기 때문이다.
본 문제에서는 Swapping이 일어나는 횟수를 판단하는 것이 관건이다.
따라서 heapsort(), heapify()에서 Swapping이 일어나는 상황을 Counting하였다. 이때, heapsort()가 진행되면서 heapify()가 호출되고, heapify()안에서도 heapify()가 재귀적으로 호출된다.
따라서 Counting 횟수가 s32_Kmax와 같을 경우 flag를 false로 설정하여 바로 탈출할 수 있도록 하였다.
정답
#include<iostream>
using namespace std;
void heapify(int32_t ars32_A[], int32_t s32_K, int32_t s32_N);
void heapsort(int32_t ars32_A[], int32_t s32_N);
void build_mean_heap(int32_t ars32_A[], int32_t s32_N);
int32_t s32_Cnt = 0, s32_Kmax, s32_Num, ars32_A[500001];
bool flag = true;
int main()
{
int32_t s32_I;
ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
cin >> s32_Num >> s32_Kmax;
for (s32_I = 1; s32_I <= s32_Num; s32_I++)
{
cin >> ars32_A[s32_I];
}
heapsort(ars32_A, s32_Num);
if (s32_Cnt < s32_Kmax)
{
cout << -1;
}
return 0;
}
void build_mean_heap(int32_t ars32_A[], int32_t s32_N)
{
int32_t s32_I;
for (s32_I = s32_N / 2; s32_I > 0; s32_I--)
{
heapify(ars32_A, s32_I, s32_N);
}
}
void heapsort(int32_t ars32_A[], int32_t s32_N)
{
int32_t s32_I;
build_mean_heap(ars32_A, s32_N);
for (s32_I = s32_N; s32_I > 1; s32_I--)
{
if (flag)
{
int32_t s32_Tmp = ars32_A[1];
ars32_A[1] = ars32_A[s32_I];
ars32_A[s32_I] = s32_Tmp;
s32_Cnt += 1;
if (s32_Cnt == s32_Kmax)
{
if (ars32_A[1] < ars32_A[s32_I])
{
cout << ars32_A[1] << " " << ars32_A[s32_I] << endl;
}
else
{
cout << ars32_A[s32_I] << " " << ars32_A[1] << endl;
}
return;
}
heapify(ars32_A, 1, s32_I - 1);
}
else
return;
}
}
void heapify(int32_t ars32_A[], int32_t s32_K, int32_t s32_N)
{
int32_t s32_Left = s32_K * 2;
int32_t s32_Right = s32_K * 2 + 1;
int32_t s32_Smaller;
if (s32_Right <= s32_N)
{
if (ars32_A[s32_Left] < ars32_A[s32_Right])
{
s32_Smaller = s32_Left;
}
else
{
s32_Smaller = s32_Right;
}
}
else if (s32_Left <= s32_N)
{
s32_Smaller = s32_Left;
}
else
return;
if (ars32_A[s32_Smaller] < ars32_A[s32_K])
{
int32_t s32_I;
int32_t s32_Tmp = ars32_A[s32_Smaller];
ars32_A[s32_Smaller] = ars32_A[s32_K];
ars32_A[s32_K] = s32_Tmp;
s32_Cnt += 1;
if (s32_Cnt == s32_Kmax)
{
cout << ars32_A[s32_K] << " " << ars32_A[s32_Smaller] << endl;
flag = false;
return;
}
heapify(ars32_A, s32_Smaller, s32_N);
}
}
'백준' 카테고리의 다른 글
| [ DP-11049 ] 행렬 곱셈 순서(C++) (0) | 2024.05.19 |
|---|---|
| [ 정렬 - 24174 ] 알고리즘 수업 - 힙 정렬 2(C++) (0) | 2024.04.03 |
| [ 트리 - 1991 ] 트리 순회(C++) (0) | 2024.04.03 |
| [ DP - 17626 ] Four Squares (2) | 2024.04.02 |
| [ DP - 2579 ] 계단 오르기 (0) | 2024.03.31 |




