| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- BFS
- MySQL
- 그래프 이론
- image processing
- 강화학습
- machine learning
- NLP
- CS285
- opencv
- CNN
- dynamic programming
- ubuntu
- 머신러닝
- Python
- hm3d
- YoLO
- UC Berkeley
- deep learning
- r-cnn
- hm3dsem
- dfs
- GIT
- AlexNet
- 딥러닝
- RL
- Reinforcement Learning
- DP
- 백준
- C++
- LSTM
- Today
- Total
JINWOOJUNG
[ DP-11049 ] 행렬 곱셈 순서(C++) 본문

접근법
연쇄적인 행렬의 곱셈 순서를 결정하는 것은 DP 문제 중 하나로, 효율적은 행렬 곱셈 순서를 결정하는 문제이다. 문제에서 언급 되었듯이 행렬의 곱셈 순서에 따라서 요구되는 계산량이 달라지기 때문에, 곱셈 연산을 최소로 하는 순서를 결정해야 한다.
가장 기본적인 행렬 곱셈의 규칙을 생각 해 보자. $A$ 행렬은 $ i by j $, $B$ 행렬은 $k by l$이라 하면, 행렬 $A,B$의 곱셈 연산이 성립하기 위해서는 $j == k$여야 하며, 계산된 행렬을 $C$라 하면, $C$의 크기는 $ i by l $이 된다.
이러한 규칙을 고려하여, 연쇄 행렬곱셈을 DP를 이용하여 해결하기 위해서 재귀 관계식을 구축하면 다음과 같다.
$$d_k = 행렬 A_k의 열의 수 /to A_k의 행의 수는 d_{k-1}$$
$$A_1의 행의 수 = d_0$$
$$1 \leq i \leq j \leq n, M[i][j] = minimum_{ 1 \leq i \leq j \leq n }(M[i][k] + M[k+1][j] + d_{i-1}d_kd_j)$$
$$ = i < j일 때, A_i 부터 A_j 까지의 행렬을 곱하는데 필요한 기본적인 곱셈의 최소 횟수$$
$$M[i][j] = 0, if i >= j$$
이에 대한 수도코드는 아래와 같고, 해당 수도코드를 기반으로 구현한 코드는 다음과 같다.

M(아래에서는 dp 2차원 배열)[i][j]이 의미하는 바는 $A_i~A_j$까지 행렬 곱셈 연산에서 요구되는 최소 곱셈 횟수이다. 따라서 $A_k$를 기분으로 곱셈 연산 순서를 분리한다면, $A_i~A_k, A_{k+1}~A_j$ 행렬 곱셈에서 요구되는 최소 곱셈 횟수와 곱해진 두 행렬의 곱셈 연산에서 요구되는 연산 $d_{i-1}*d_k*d_j$를 더한 값을 최소로 하는 $k$를 찾으면 된다.
#include<iostream>
using namespace std;
int dp[500][500];
int p[500][500];
int d[500];
const int MAX = 9999999;
void order(int i, int j);
int main()
{
ios::sync_with_stdio(false);
cin.tie(NULL);
int N, i, j,k, diagonal, tmp;
cin >> N;
for (k = 0; k < N; k++)
{
cin >> i >> j;
d[k] = i;
if (k+1 == N)
{
d[k + 1] = j;
}
}
for (diagonal = 0; diagonal < N; diagonal++)
{
for (i = 1; i <= N - diagonal; i++)
{
j = i + diagonal;
if (i == j)
{
dp[i][j] = 0;
continue;
}
dp[i][j] = MAX;
for (k = i; k < j; k++)
{
tmp = dp[i][k] + dp[k + 1][j] + d[i - 1] * d[k] * d[j];
if (dp[i][j] > tmp)
{
dp[i][j] = tmp;
p[i][j] = k;
}
}
}
}
printf("%d\n",dp[1][N]);
return 0;
}
해당 수도코드를 기반으로 구현하게 된다면, 약간의 불필요한 계산이 요구된다. 이중 for문을 돌면서 접근하여 최소 연산량을 구하는 DP 테이블을 채우게 되는데, 이때의 테이블을 접근하는 Index를 출력하면 다음과 같다.
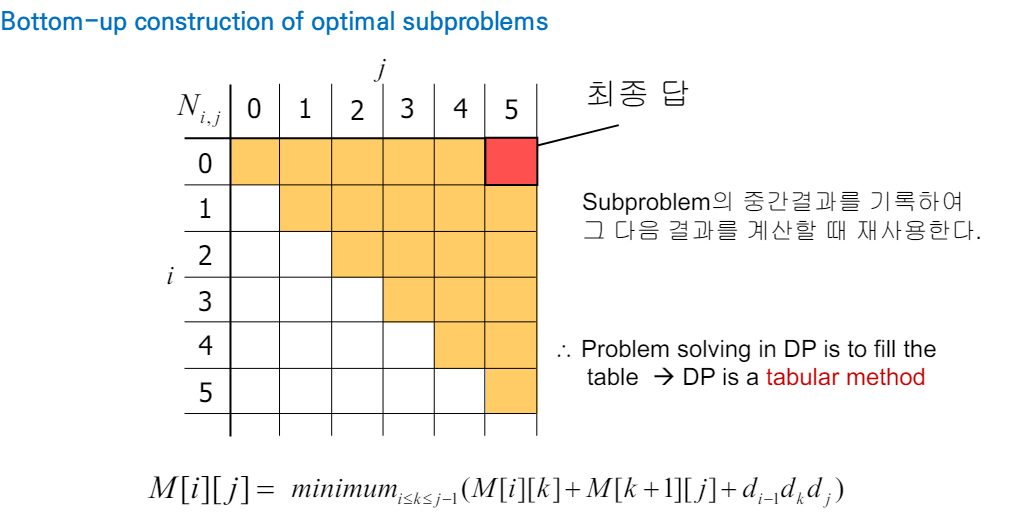
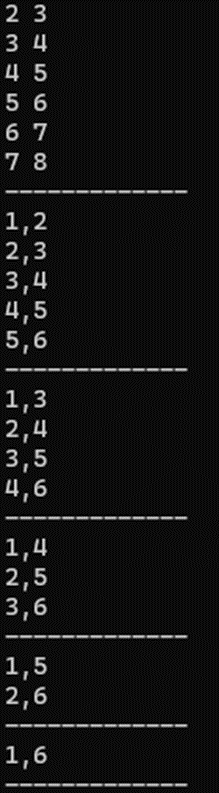
반복문을 도는 첫번째, 두번째 과정에서 불필요한 접근을 2번씩 하고 있는 것을 확인할 수 있다. 이때, 해당 알고리즘을 기반으로 접근하는 코드 구현을 위해선, 2번씩 접근해야 하지만 서로 다른 for문 과정에서 접근하기에 더 많은 연산 시간을 요구한다. 따라서 이를 수정하면 다음과 같다.
정답
#include <iostream>
#include <cstdio>
#include <limits.h>
using namespace std;
const int MAXN = 500;
const int INF = INT_MAX;
int dp[MAXN][MAXN];
int p[MAXN][MAXN];
int d[MAXN + 1];
int main() {
int N,i,j,k,cost,diagonal;
cin >> N;
// 행렬의 차원을 입력받음
for (k = 0; k < N; k++) {
cin >> i >> j;
d[k] = i;
if (k == N - 1) {
d[k + 1] = j;
}
}
for (i = 1; i <= N; i++) {
dp[i][i] = 0;
}
// dp 테이블 채우기
for (diagonal = 2; diagonal <= N; diagonal++) {
for (i = 1; i <= N - diagonal + 1; i++) {
j = i + diagonal - 1;
dp[i][j] = INF;
for (k = i; k < j; k++) {
cost = dp[i][k] + dp[k + 1][j] + d[i - 1] * d[k] * d[j];
if (cost < dp[i][j]) {
dp[i][j] = cost;
p[i][j] = k;
}
}
}
}
// 최소 비용 출력
printf("%d\n", dp[1][N]);
return 0;
}
접근하는 Index를 동일하게 출력 해 보면, 하나의 for문 안에서 두 과정에 동시에 진행되기 때문에 연산속도가 빨라 졌음을 예상할 수 있다.
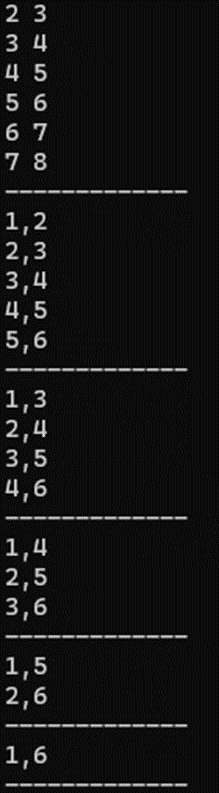

'백준' 카테고리의 다른 글
| [ DP - 11404 ] 플로이드(C++) (0) | 2024.05.23 |
|---|---|
| [ DP - 12865 ] 평범한 배낭(C++) (0) | 2024.05.20 |
| [ 정렬 - 24174 ] 알고리즘 수업 - 힙 정렬 2(C++) (0) | 2024.04.03 |
| [ 정렬 - 24173 ] 알고리즘 수업 - 힙 정렬 1(C++) (2) | 2024.04.03 |
| [ 트리 - 1991 ] 트리 순회(C++) (0) | 2024.04.03 |




