| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 그래프 이론
- C++
- dfs
- AlexNet
- LSTM
- DP
- hm3d
- NLP
- MySQL
- Reinforcement Learning
- image processing
- 딥러닝
- Python
- GIT
- YoLO
- dynamic programming
- CNN
- ubuntu
- opencv
- 백준
- 머신러닝
- hm3dsem
- RL
- deep learning
- CS285
- machine learning
- BFS
- 강화학습
- r-cnn
- UC Berkeley
- Today
- Total
JINWOOJUNG
[ DP - 12865 ] 평범한 배낭(C++) 본문

접근법
또 다시 DP 문제이다.
각 물품에는 Weight, Value가 존재하고, 배낭이 버틸수 있는 Limit Weight는 K로 제한되어 있다. 따라서 목표는 Weight Sum이 K 이하인 최대한의 가치합을 가지는 물건들을 선택해야 한다.
최적성의 원리를 적용하여 해당 문제를 Dynamic Programming으로 해결할 수 있는지 살펴보자.

우리는 위와 같은 Table을 생각할 수 있다. 제한되는 무게에 따라서 각 물품을 담을 수 있는지가 결정되고, 그에 따라서 Value의 최대 합이 달라지기 때문이다. 따라서 해당 Table의 각 원소는 Limit Weight보다 작은 범위에서 고려되는 물품들의의 개수에 따른, 담을 수 있는 물품들의 가치 최대합이 들어가게 된다.
따라서 각 물품들의 Weight와 Value를 저장하는 Table이 추가적으로 요구된다. 이를 ars32_Weight, ars32_Value 2차원 배열이라 하자.


자 그럼 Table을 채워보자. Limit Weight가 1,2인 경우는 물품의 최소 Weight가 3이기 때문에 모두 0이다.
Limit Weight가 3인 경우는 2개의 물품까지 고려한 경우 각 물품의 Weight가 6,4이기 때문에 모두 0이고, 3번째 물품이 고려되는 순간 3번째 물품의 Value인 6이 된다.
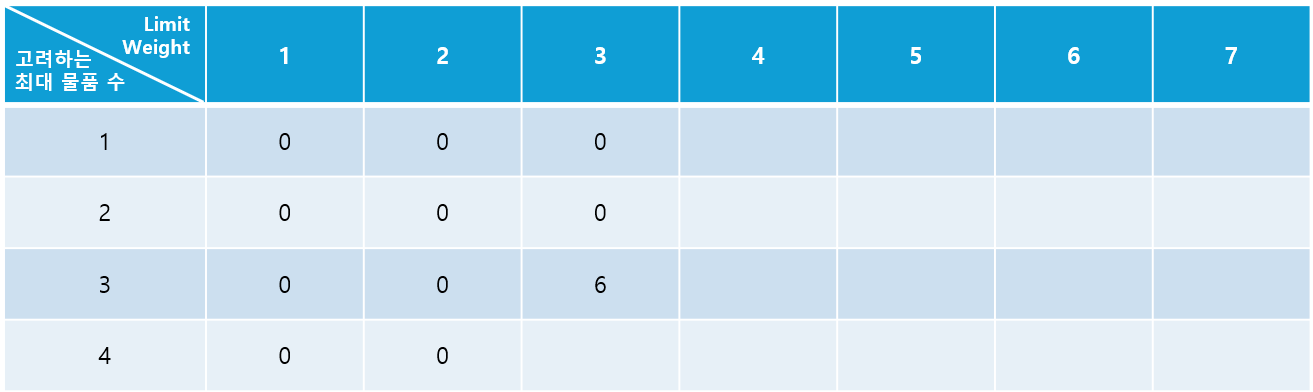
4번째 물품까지 고려해도, 4번째 물품의 Weight는 5이기 때문에, Value의 최대합은 6이 된다. 이 과정에서 우리는 만들어 둔 Table을 이용해야 하는데, 각 Table이 의미하는 바가 Value의 최대합이기 때문에, 해당 물품의 Weight가 Limit Weight를 넘어간다면, 이전 물품까지 고려했을 때의 Value 최대합을 가져오면 된다. 현재 Table의 Index가 $DP[i][j]$라 하면, $DP[i-1][j]$의 값을 가져오면 된다.
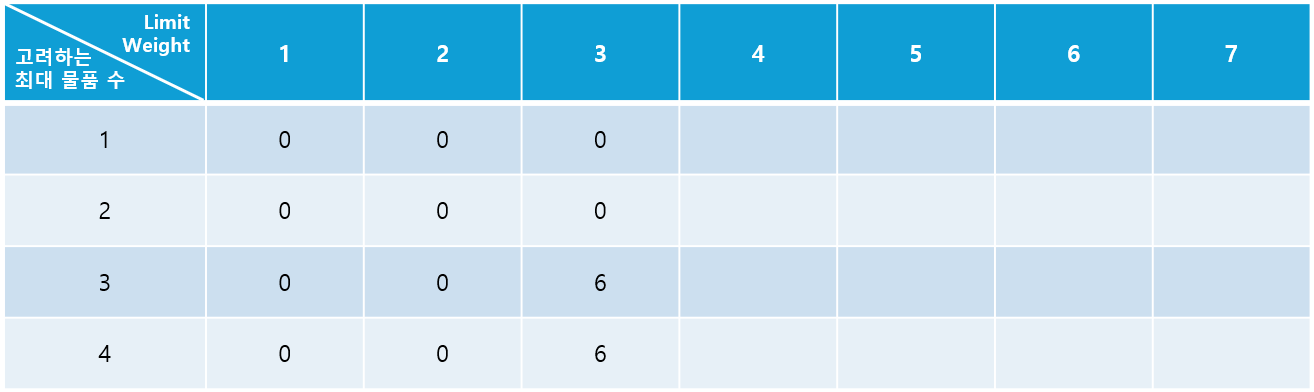
Limit Weight가 4가 되는 순간, 가능한 물품의 Index는 2와 3이 된다. 따라서 Limit Weight보다 첫번째 물품의 무게가 크기 때문에, $DP[1][4] = DP[1-1][4] = DP[0][4] =0$이 된다. 2번째 물품까지 고려하는 경우 ars32_Weight[2] = 4이기 때문에 Limit Weight 조건을 만족하여 해당 물품의 Value인 ars32_Value[2] = 8이 $DP[2][4]$가 된다.
3번째 물품까지 고려한 경우 3번째 물품도 Limit Weight를 만족하게 된다. 따라서 이제부터는 비교가 필요하다. 앞서 말한 것 처럼, DP의 값은 해당 인덱스의 물품까지 고려했을 때의 Value 최대합이다. 새롭게 고려되는 물품의 Value가 더 크다면, 해당 Value가 DP의 값이 되어야 하고, 그렇지 않다면 이전 값을 가져와야 한다. 따라서 다음과 같은 조건문이 필요하다.
$$ DP[i][j] = max(DP[i-1][j] , ars32_Value[i]) $$
따라서 $$DP[3][4] = max(8, 6) = 8$$이 된다.

따라서 Limit Weight가 6인 경우 까지는 위의 조건만 고려하면 해결할 수 있다.

하지만 Limit Weight가 7인 경우를 보자.
1번 물품까지 고려했을 때의 Value의 최대합은 ars32_Value[1] = 13이다. 2번 물품까지 고려했을 때의 Value 최대합은 2번 물품의 Value가 12이기 때문에 $max$ 조건에 걸려 13이 된다.
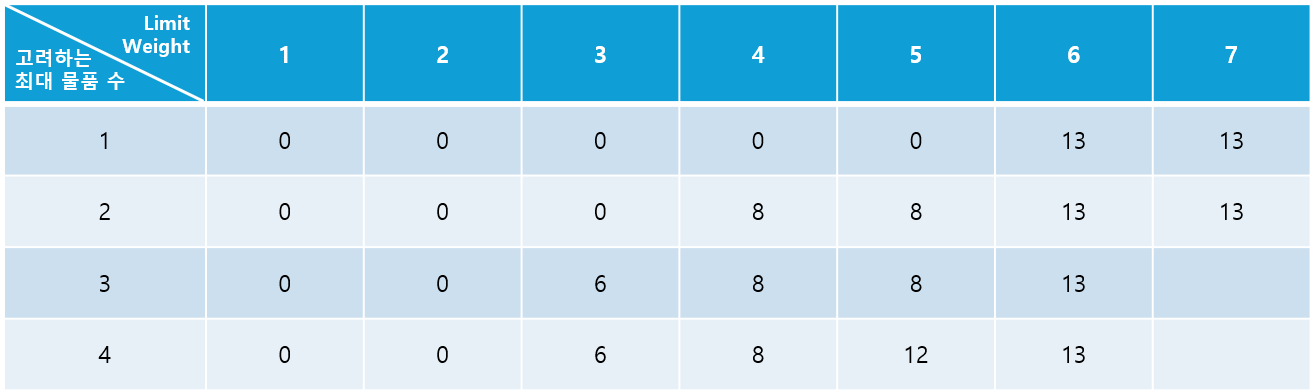
3번 물품까지 고려했을 때의 Value 최대합은 3번 물품의 Value가 6이기 때문에, $max$ 조건에 걸려 13이다..라고 하면 안된다. ars32_Weight[2] = 4, ars32_Weight[3] = 3 이기 때문에, 2,3번 물품을 모두 담아도 Limit Weight 조건에 걸리지 않으므로 최대합은 13이 아닌 ars32_Value[2] + ars32_Value[3] = 14가 되어야 한다.
그렇다면, 현재 새롭게 고려되는 물품의 무게를 제외하였을 때, 이전 까지 고려되었던 물품들을 고려한 Value의 최대합이 필요하다. 그리고 우린 특정 인덱스의 물품까지 고려하였을 때, Limit Weight를 만족하는 Value의 최대합을 $DP$ 2차원 행렬에 저장해 왔으니 이를 이용하면 된다. 현재 새롭게 고려되는 물품을 제외하여야 하므로 $DP$ 행렬의 행 Index는 i-1이 된다. 또한, Limit Weight는 내 무게를 빼야 하므로, $DP$ 행렬의 열 Index는 j-ars32_Weight[i]가 된다. 그 위치의 Value의 최대합과 현재 물품의 Value를 더한 값과, Limit Weight가 j일 때, 이전 물품까지 고려한 Value의 최대합을 비교한다면 정확한 값을 찾을 수 있다.
$$ DP[i][j] = max(DP[i - 1][j - ars32\_Weight[i] + ars32\_Value[i], DP[i - 1][j]) $$

정답
#include<iostream>
#include <algorithm>
using namespace std;
int32_t ars32_Weight[101] = { 0 };
int32_t ars32_Value[101] = { 0 };
int32_t ars32_DP[101][100001];
int main()
{
int32_t s32_I, s32_J, s32_K, s32_Limit, s32_Num;
// Input Data
cin >> s32_Num >> s32_Limit;
for (s32_K = 1; s32_K <= s32_Num; s32_K++)
{
cin >> ars32_Weight[s32_K] >> ars32_Value[s32_K];
}
// DP 배열 초기화
for (s32_I = 0; s32_I <= s32_Num; s32_I++) {
for (s32_J = 0; s32_J <= s32_Limit; s32_J++) {
ars32_DP[s32_I][s32_J] = 0;
}
}
for (s32_J = 1; s32_J <= s32_Limit; s32_J++)
{
for (s32_I = 1; s32_I <= s32_Num; s32_I++)
{
// Limit Weight에 걸려서 담을 수 없는 경우
if (ars32_Weight[s32_I] > s32_J)
{
ars32_DP[s32_I][s32_J] = ars32_DP[s32_I - 1][s32_J];
}
// 담을 수 있는 상황
else
{
// s32_I번째 물건 하나만 담는 가치와 내 무게를 뺀 제한 무게 내에서의 최대 가치를 비교
ars32_DP[s32_I][s32_J] = max(ars32_DP[s32_I - 1][s32_J - ars32_Weight[s32_I]] + ars32_Value[s32_I], ars32_DP[s32_I - 1][s32_J]);
}
}
}
printf("%d\n", ars32_DP[s32_Num][s32_Limit]);
return 0;
}'백준' 카테고리의 다른 글
| [ DP ] 조약돌 놓기(C++) (0) | 2024.05.24 |
|---|---|
| [ DP - 11404 ] 플로이드(C++) (0) | 2024.05.23 |
| [ DP-11049 ] 행렬 곱셈 순서(C++) (0) | 2024.05.19 |
| [ 정렬 - 24174 ] 알고리즘 수업 - 힙 정렬 2(C++) (0) | 2024.04.03 |
| [ 정렬 - 24173 ] 알고리즘 수업 - 힙 정렬 1(C++) (2) | 2024.04.03 |




