| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- machine learning
- C++
- 그래프 이론
- RL
- 백준
- GIT
- opencv
- ubuntu
- CNN
- BFS
- 딥러닝
- r-cnn
- AlexNet
- YoLO
- dfs
- Python
- hm3d
- image processing
- Reinforcement Learning
- NLP
- 머신러닝
- CS285
- MySQL
- 강화학습
- LSTM
- deep learning
- dynamic programming
- hm3dsem
- DP
- UC Berkeley
- Today
- Total
JINWOOJUNG
[ 영상 처리 ] Ch8. Clustering and Segmentation(2) 본문
본 영상 처리 개념과 기법들에 대한 공부를 진행하면서 배운 내용들을 중심으로 정리한 포스팅입니다.
책은 Computer Vision: Algorithms and Applications를 기반으로 공부하였습니다.
또한, 인하대학교 박인규 교수님의 디지털 영상 처리 과목을 기반으로 제작된 포스팅입니다.
Before This Episode
[ 영상 처리 ] Ch8. Clustering and Segmentation(1)
본 영상 처리 개념과 기법들에 대한 공부를 진행하면서 배운 내용들을 중심으로 정리한 포스팅입니다. 책은 Computer Vision: Algorithms and Applications를 기반으로 공부하였습니다.또한, 인하대학교 박
jinwoo-jung.com
Segmentation
Segmentation은 영역화(분류)라는 의미로 말 그대로 영역을 분리하는 것이다. 특정한 영상이 있으면 해당 영상 안에는 다양한 객체들이 존재한다. 우리는 각 객체들이 차지하고 있는 영역이 궁금하다. 그렇기 때문에, 해당 객체에 속하는 분포(데이터)를 그룹화 하기 위한 Clustering 기법을 먼저 배운 것이다.

Segmentation을 배우기 전, Classification, Detection에 대하여 알아보자.
먼저 Classification은 영상 전체의 범주(클래스)를 분류하는 것이다. 왼쪽 영상을 보면 누가 봐도 "고양이"에 대한 영상이다. 이처럼 영상 자체의 범주를 분류하는 과정에 Classification이다.
다음으로 Segmentation 중 Semantic Segmentation은 픽셀 자체를 문맥에 맞게 분류(영역화)하는 것이다. 조금 다르게 해석하자면 주어진 Class에 맞는 픽셀끼리 분류하는 것이다. 아래와 같이 4개의 Class가 주어지면, 각 픽셀이 해당되는 Class에 따라 다르게 분류된다.
Object Detection은 말 그대로 객체 검출이다. 영상 내 객체를 검출하여 해당 객체에 해당하는 영역(위치)를 검출하는 것이다.
마지막으로, Instance Segmentation은 Semantic Segmentation과 Object Detection을 동시에 수행하는 과정으로, 같은 Class 객체의 픽셀 안에서 Instance에 따라 서로 다르게 구분하는 과정이다. 마지막 그림에서 단순히 Dog, Cat이라는 Class에 대하여 Semantic Segmentation을 수행한다면 서로다른 두 강이지는 모두 "Dog" 클래스에 속하기 때문에 동일하게 칠해질 것이다. 반면, Instance Segmentation은 검출한 객체에 대하여 서로 다르게 영역화를 진행한다.
Image Segmentation Methods
영상에서의 Segmentation은 Edge 기반과 영역 기반으로 나눌 수 있다.
Edge-based Image Segmentation

Edge 기반의 Segmentation은 Contour를 찾는 것이 중요하다. Countour란 연속적으로 연결된 Edge를 의미한다. Contour를 구한 Map을 기반으로 Segmentation을 진행하면 오른쪽과 같다. 굵직한(강한) Edge를 기반으로 영역화를 진행한 것으로 예측된다.
Contour - Active Contour Models : Snakes

Contour를 찾는 첫번째 방법은 Snakes이다. Snakes는 Contour가 능동적으로 모양을 변화시켜 가면서 최적의 Contour를 찾는 과정이다. 가는 실선인 초기 Contour가 가운데 점선처럼 변형되어 가면서 우리가 찾고자 하는 실선의 Contour에 맞게 변한다. 해당 움직임은 Gradient를 구해 방향을 설정하여 최적의 Contour로 변화한다고만 이해하자.
실제로 최적의 Contour의 밖에서 안쪽으로 변화하는 과정은 Outlier에 취약하다. 따라서 아래와 같이 최적의 Contour 안에서 밖으로 뻗어나가면서 최적의 Contour를 찾는 방법이 주로 쓰인다.
Contour - Active Contour Models : Level Sets


Level Sets는 Contour를 수학적 방식을 통해 파라미터를 조절 해 나가면서 찾아가는 모델이다. 수학적인 모델이 있지만, $\phi(x,y)$를 변화 해 가면서 Contour를 찾아 간다고만 이해하자. 영상을 보면 회색 선과같이 방해 요소들이 존재하지만, 강건하게 Contour를 찾을 수 있다는 장점이 있다.
Region-based Image Segmentation


Region-based Image Segmentation은 영상에서 유사한(같은 Class에 속하는) Pixel을 영역화(Grouping)하는 방법이다. 대표적으론 Mean-Shift Clustering 기법을 이용하여 Segmentation을 수행하면 된다. 왼쪽은 색상과 위치, 오른쪽은 Texture과 위치를 기반으로 Clustering하여 Segmentation 한 결과이다.
큰 Pipeline을 구상 해 본다면, 앞으로 배울 Mean Shift Algorithm으로 Pixel Grouping(Clustering)을 진행하여 같은 Cluster(Region)에 속하는 픽셀끼리 Segmentation 하는 것이다.
Mean Shift Algorithm

Mean Shift Algorithm은 non-parameteric density의 modes(peak)를 찾는 과정을 포함한다. 이때, non-parameteric은 오직 주어진 데이터에서 확률을 계산하여 직접 통계적으로 분석하는 방법이다. 왼쪽 상단의 원본 영상을 LCV Color Model로 변환하여 모든 픽셀에 대하여 분포도를 계산하면 왼쪽 하단과 같다. 이에 대하여 Density를 구하면 오른쪽 상단과 같고, 우리는 modes(peaks)를 찾을 수 있다. 따라서 색상 분포의 Density를 따르는 Modes를 찾아 Clustering을 수행하면 오른쪽 하단과 같다.
그렇기 때문에, K-Means Clustering과 달리 Mean Shift Algorithm은 Clustering Num을 사전에 정의할 필요가 없다.
Kernel Density Estimation(KDE)
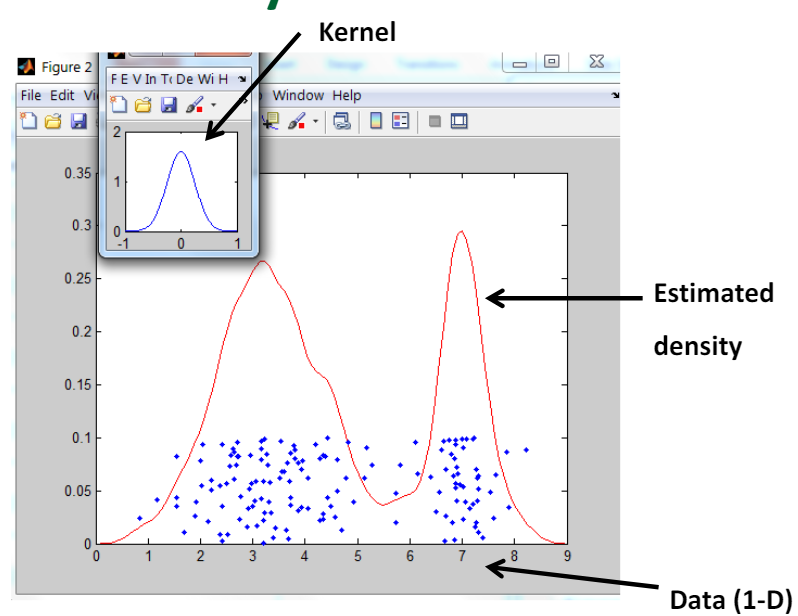
수많은 데이터에서 Local Maximum이 아닌 Global Maximum(Modes)를 찾아야 한다. 수많은 데이터를 한번에 처리할 수 없기에 Region of Interest(RoI)를 설정하고, 해당 RoI(Kernel) 내부에서 Kernel Function을 기반으로 Kernel을 이동시킬 Center of Mass(무게중심)을 구한다. 일반적으론 Gaussian Kernel Function을 사용하여 Kernel 내 데이터의 분포를 잘 표현하는 Gaussian을 생성한 뒤, 중심에 가까울수록 더 큰 가중치를 주어 무게중심을 계산한다. 이를 통해 Outlier에 강건하고, 더 부드럽게 Kernel를 이동시킬 수 있으며, Data의 Density를 반영하기 때문에 정확한 Modes를 찾아서 움직일 수 있다.


실제로 Kernel(RoI)이 Modes를 찾아 움직이는 과정을 살펴보자. Kernel 내의 영역(RoI)는 파란색 원으로 표현된다. 해당 데이터의 밀도(분포)를 최대한 반영하여 생성한 KDE의 peak가 파란색 원점과 같고, 해당 영역 데이터의 무게중심이 주황색 원점과 같다면, 해당 방향으로 peak점을 이동시킨다. 이후 변경된 RoI 내의 데이터에 대하여 다시 무게중심을 이동하고, KDE의 peak점을 다시 이동시킨다.


만약 Mean Shift Vector의 변화량이 수렴하게 된다면, 해당 peak점이 결국 Modes가 되어 Density의 Peak 점이 된다.


이때, RoI 내Data에 대하여 질량 중심 계산 시 중심으로 부터 떨어진 거리에 따라 Weight를 부여하기 위하여 Gaussian Distribution을 계산한다. $x_{new}$를 계산하는 분자는 $x_i$의 weight를 이동 전 peak $x$로 부터 현재 데이터와 떨어진 거리를 고렬하는 Gaussian Weight를 계산하여 부여하였으며, 분모는 Sum of Weight이다(정규화).
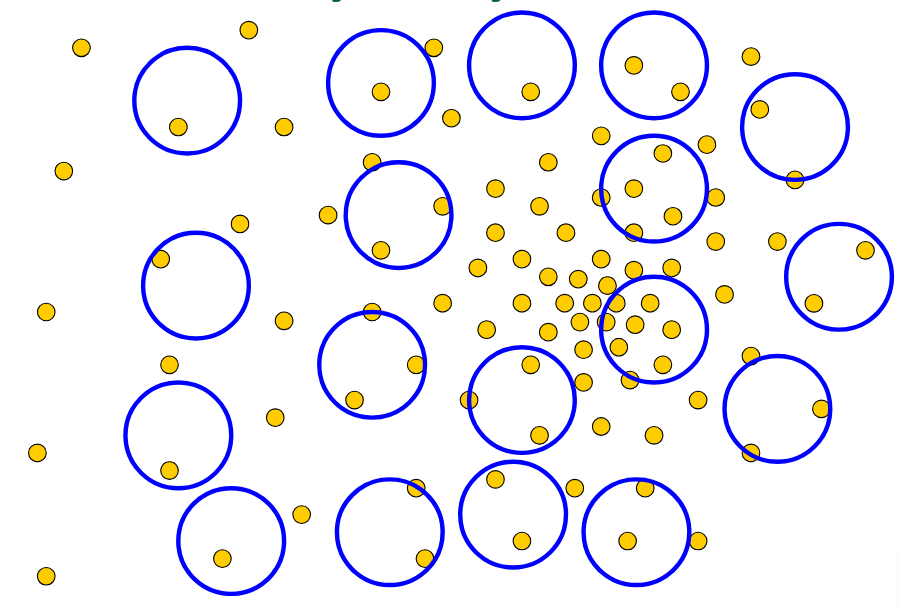
해당 과정을 1번만 하는 것이 아닌 다양한 부분에서 진행하여 Modes를 찾아낸다. 즉, 모든 Data가 잠재적인 Modes라고 가정하고 앞서 설명한 Mean Shift Algorithm을 기반으로 최적의 Modes를 찾아 나간다.
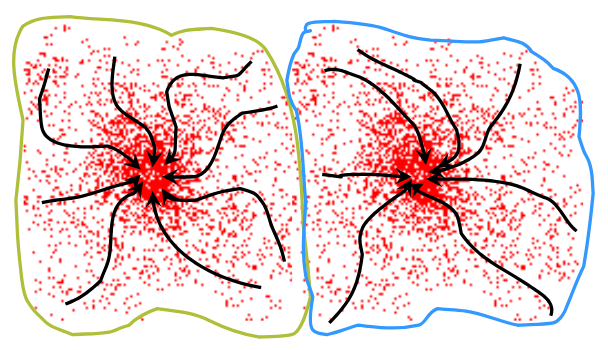
다양한 시작점에서 Mean Shift Algorithm을 통해 생성된 Mean Shift Vector들을 연결하면 위의 검은색으로 표현한 Attraction Basin 즉, 시작점에서 부터 Modes 까지의 Trajectory를 생성할 수 있다. 따라서 우리는 하나의 모드에 속하는 모든 Attraction Basin의 Points에 대하여 Clustering을 수행하면 된다.

앞서 소개한 과정을 다시 이해 해 보면, 왼쪽 상단의 Data에 대하여 Mean Shift를 수행하면, 아래와 같이 7개의 Peaks를 생성하고, 각 Peak에 해당하는 Attraction Basin을 Clustering 하면, 7개의 Clustering이 생성된다. 이처럼 자동적으로 Clustering 되기 때문에, $K$를 지정해 줄 필요가 없다(Unsupervised-Learning).

따라서 Hyper Parameter는 Kernel과 Bandwidth, 앞선 예를 들면 Gaussian과 $\sigma$를 선정 해 주는 것 밖에 없다. 이때, $\sigma$를 줄인다면, Kernel Size(RoI) 역시 줄어들기 때문에 Local Maximum에 빠질 수 있다.

그렇다면, 밀도를 계산하기 위한 Data(Feature)는 무엇으로 할까? 일반적으로 색상, Texture(반복되는 패턴) 등으로 설정하며, 추후 Clustering을 위한 해당 픽셀의 Position 정보도 함께 저장한다. 단일 Feature가 아닌 다중 Feature를 이용한다면 그 Scale, 차원이 다르기 때문에 Feature를 위한 Kernerl size $K_f$, Pixel Position을 위한 Kernel Size $K_s$를 정해줘야 한다.

장점
RoI 내의 Data를 기반으로 Mean Shift를 수행하기 때문에 Outlier의 큰 영향을 받지 않는다.
Clustering 개수를 사전에 정의해 주지 않아도 된다.
단점
Kernel Size를 결정 해 줘야 하며, Data와 Dimension에 따른 많은 연산량을 요구한다.
'2024 > Study' 카테고리의 다른 글
| [ GRAPH ] Topological Sorting (0) | 2024.06.02 |
|---|---|
| [ 영상 처리 ] Ch8. Clustering and Segmentation(3) (0) | 2024.06.01 |
| [ 영상 처리 ] Ch8. Clustering and Segmentation(1) (0) | 2024.05.29 |
| [ 영상 처리 ] Ch7. Color Image Processing (0) | 2024.05.29 |
| [ 영상 처리 ] Ch9. Local Feature Detection and Matching(4) (0) | 2024.05.28 |




