| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- GIT
- machine learning
- 백준
- RL
- 머신러닝
- BFS
- Reinforcement Learning
- 딥러닝
- 강화학습
- hm3dsem
- Python
- NLP
- image processing
- AlexNet
- hm3d
- 그래프 이론
- MySQL
- dynamic programming
- CNN
- YoLO
- UC Berkeley
- ubuntu
- C++
- LSTM
- r-cnn
- CS285
- deep learning
- dfs
- opencv
- DP
- Today
- Total
JINWOOJUNG
[ GRAPH ] Topological Sorting 본문
Topological Sorting(위상 정렬)을 배우기 전, 비순환 유향 그래프에 대해서 알아보자. 구체적인 코드보다는 동작과정에 집중한다.
Directed Acyclic Graph(DGA) 비순환 유향 그래프
DAG는 싸이크링 없는 유향 그래프이다.
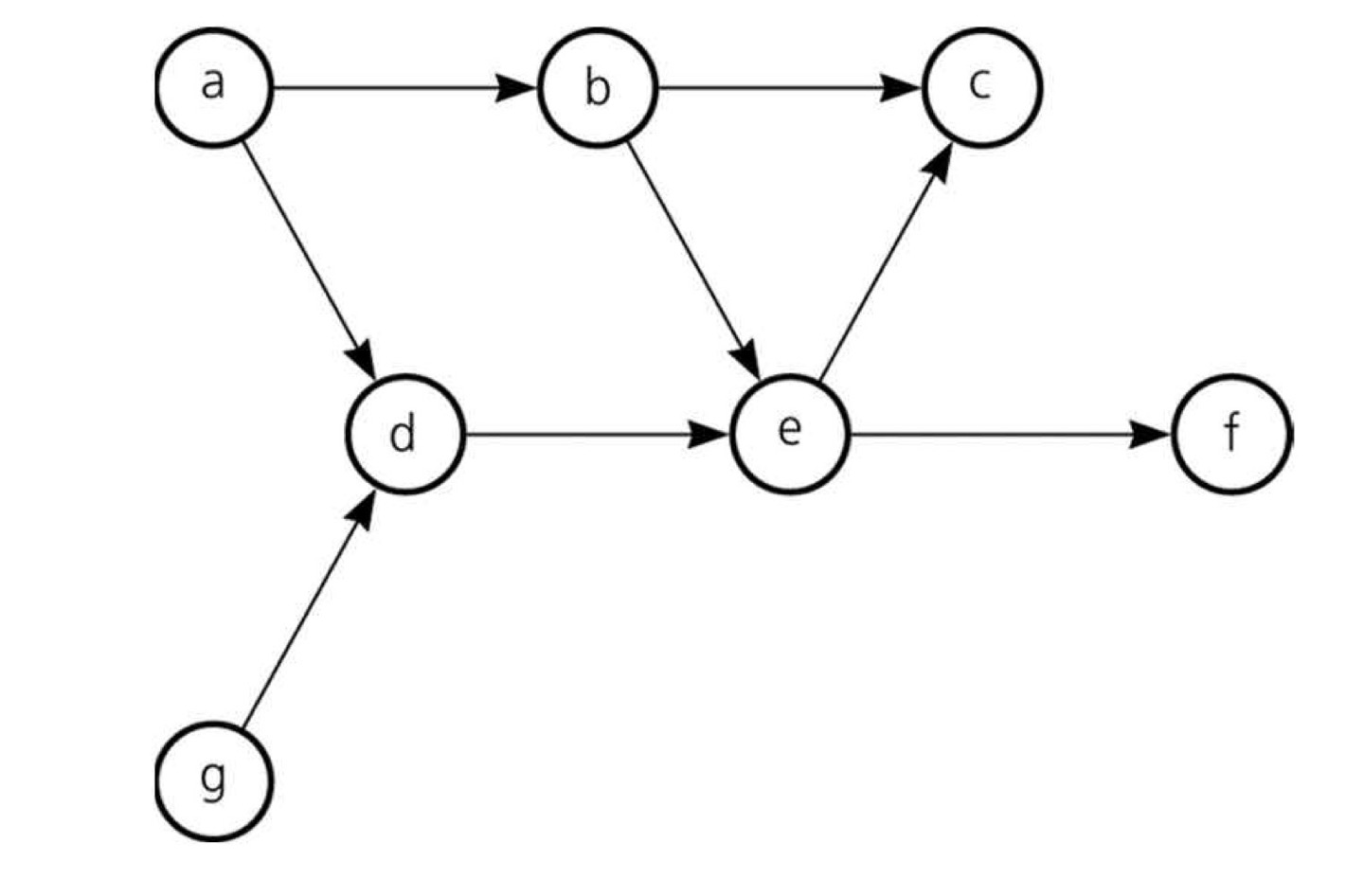

왼쪽 그래프가 DAG에 해당된다. 만약 $b Node \to c Node$의 방향이 반대면, 오른쪽과 같이 Cycle이 발생하게 된다. 이와 같은 Cycle이 존재하는 유향 그래프에서는 Topological Sorting을 적용할 수 없다.
Topological Sorting 위상정렬
위상 정렬은 DAG에서 정점들을 선형으로 정렬하는 것이다. 이때, $x Node \to y Node$의 간선이 존재하면, $x Node$는 $y Node$보다 앞에 위치하는 순서로 정렬된다.
하나의 Node에서 다중 Node로의 간선이 존재할 수 있기 때문에, 일반적으로 DAG에 대하여 다수의 위상 순서가 존재한다.

위에서 언급한 DAG에 대한 위상정렬 중 2가지이다. $a Node$와 연결된 노드가 $b,d Node$이기 때문에 그에 따라 순서가 다르게 정렬됨을 확인할 수 있다.
Topological Sorting Algorithm 1

특정 노드로 들어오는 간선을 진입간선, 특정 노드에서 다른 노드로 나가는 간선을 진출간선이라 하자. 첫번째 Algorithm은 진입 간선이 없는 노드 $u$를 선택한다. $u Node$를 방문했음을 표현하기 위해 $A$ Array의 i번째 Index에 $u$를 집어 넣는다. 그리고 $u Node$와 $u Node$의 진출간선을 DAG에서 제거한다. 이를 모든 Node를 방문할 때 까지 반복한다.
위 알고리즘을 기반으로 하여 Topological Sorting을 수행하기 위해서는, 각 노드에 대하여 진입 간선의 갯수를 저장한 배열과 방문 순서를 저장할 배열이 요구된다. 이를 $A$와 $InputEdge$ 배열로 선언하고 Sorting 과정을 서술할 것이다. 만약, 진입 간선이 0인 노드가 여러개일 경우 Random Choice를 한다. 그렇기 때문에 다양한 정렬 순서가 존재한다.
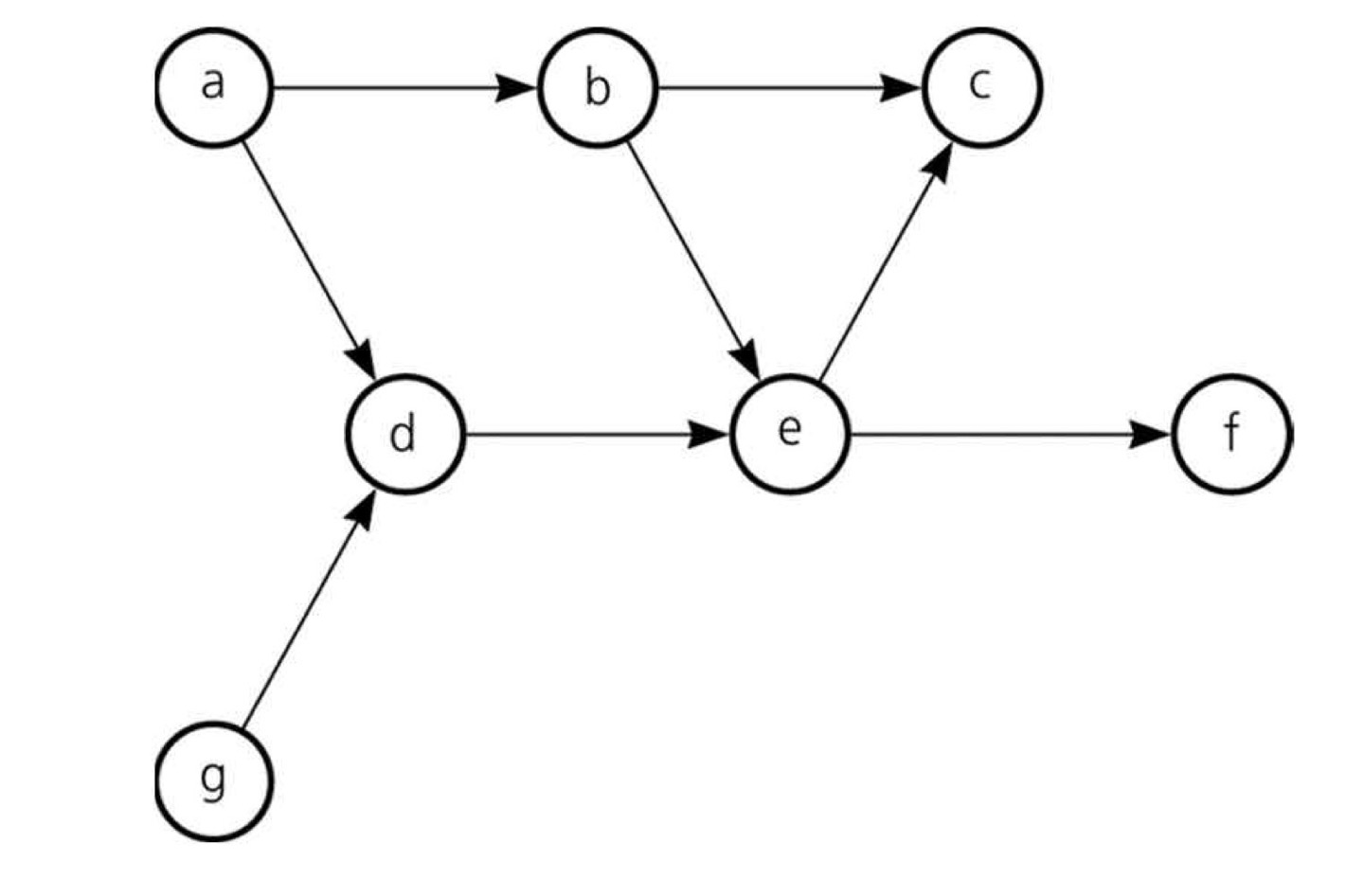
위 DAG를 기반으로 $InputEdge$ Array를 작성하면 다음과 같다.

$a, g Node$가 모두 0이므로 Random Choice를 진행한다. $g Node$를 방문했다고 하면, $g Node$를 지운 뒤 $d Node$의 진입 간선을 하나 지운다.

$a Node$의 진입 간선이 0개이므로 $a Node$와 진입 간선을 모두 지운다.

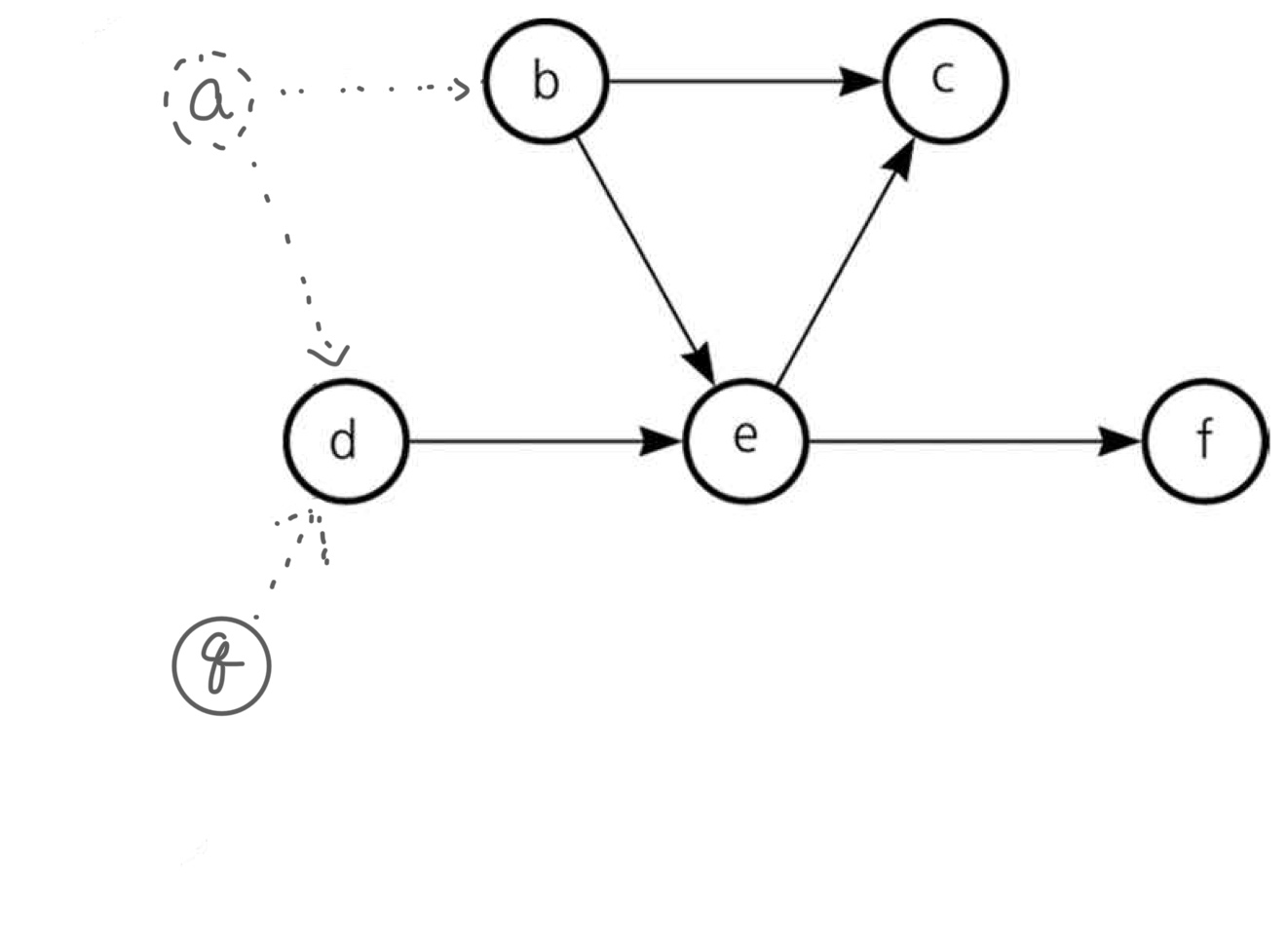
현재 위와 같은 상황이다. $a,g Node$는 이미 방문한 상황이므로 각 Node와 진출 간선은 모두 방문(제거)한 상황이다. 현재 $b, d Node$ 모두 진입 간선이 0개이므로 Random Choice하여 $b Node$를 선택하였다.

진입 간선이 0개인 노드는 $d$노드이다. $d Node$를 방문하자.

다음은 $e Node$이다.

나머지 두 노드 모두 진입 간선이 0이므로 Random Choice하여 $c, f Node$ 순서데로 방문했다고 가정하자.

더이상 방문하지 않은 노드가 없기 때문에 종료한다.
첫번째 Topological Sorting 알고리즘을 정리하자면, 진입 간선이 0인 노드를 선택하여 방문하고, 해당 노드를 삭제함과 동시에 진출 간선을 고려하여 연결된 Node의 진입 간선 개수를 1개 줄인다. 만약, 진입 간선이 0인 노드가 여러개이면 Random Choice를 진행한다. 방문한 순서를 $A$ Array에 저장하며, 방문한 순서데로 Array의 뒤로 추가된다. 모든 Node를 진행할 때 까지 위 과정을 반복한다.
Topological Sorting Algorithm 2(Using DFS)

DFS를 사용하는 두번째 알고리즘은 진입 간선을 저장하는 배열이 필요 없다. 단지 DFS만 잘 수행하면 된다.
- 방문하지 않은 Node 중 Random Choice 된 Node에 대해서 DFS를 수행한다.
- DFS 수행
- 시작 정점에서 탐색 시작
- Edge를 기반으로 다음 정점 방문
- 더 이상 방문할 Node가 없는 경우 해당 노드를 $A$ 리스트의 앞에 추가
- 역 추적을 통해 이전에 지나온 정점들로 이동하여 3번 과정 반복
- 역 추적 과정에서 이전에 지나온 정점들이 역 순서데로 더 이상 방문할 Node가 없는 Node가 됨(이미 방문한 노드를 고려 x)
- 역 추적 과정에서 방문하지 않은 다른 Node가 있으면 방문(DFS)
- 1,2 과정을 모든 노드를 방문할 때 까지 반복
앞으로 더 이상 방문할 Node가 없는 Node를 Terminal Node라 칭할 것이다.

Random Choice를 하여 $b Node$를 선택했다고 하자. DFS를 수행하면 순서가 중요하기 때문에, $c, e$순서데로 stack에 쌓인다. 우리가 알고 있는 DFS는 다음으로 stack에 top에 있는 $e Node$를 빼내면서 방문했다고 처리하지만, Topological Sorting에서는 $e Node$는 Stack에 놔두고, $e Node$에서 방문 가능한 Node들을 stack에 추가한다.
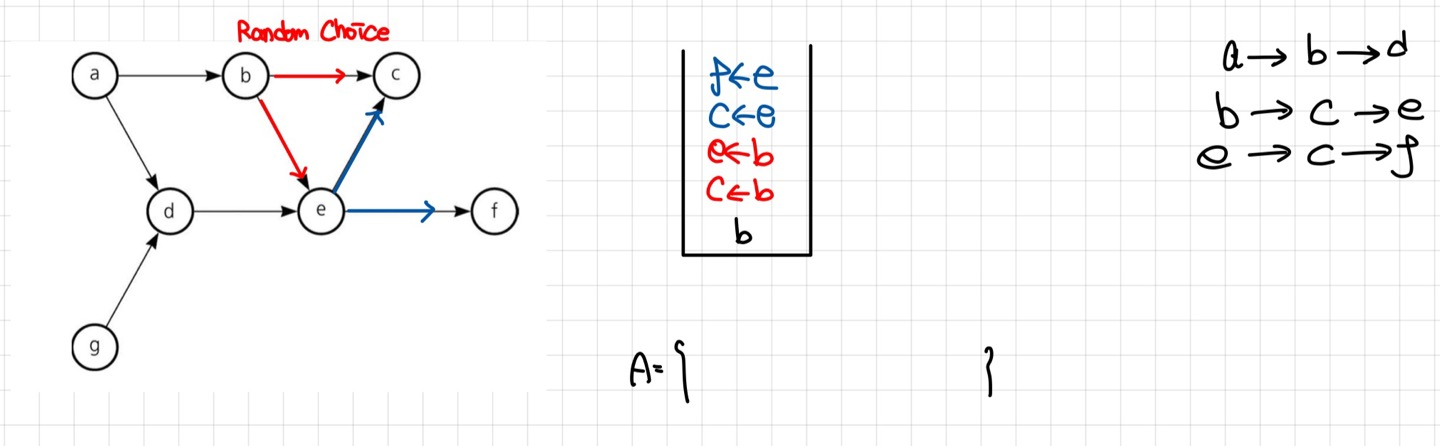
현재 stack의 top은 $f node$로 Terminal Node이다. 따라서 $f Node$를 방문하였기에 stack에서 빼낸 뒤 $A$ Array의 앞쪽에 추가한다. 이후 역 추적을 진행한다.
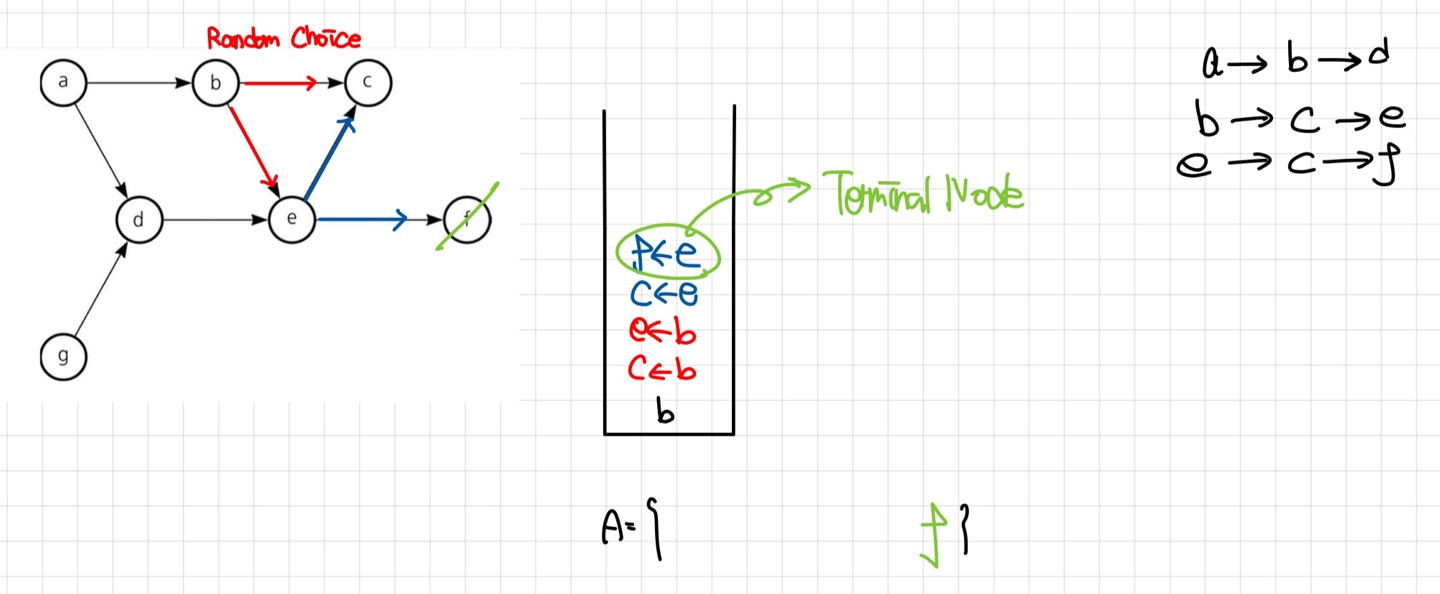
역 추적한 현재 위치는 $e Node$이지만, Terminal Node가 아니다. 현재 stack 내에 $e \to c Node$가 남아있으므로 $c Node$로 이동한다. 이후 $c Node$는 Terminal Node이므로, 방문하였기에 stack에서 빼낸 뒤 $A$ Array의 앞쪽에 추가한다.

이때, 방문한 Node를 $A$ Array의 앞쪽에 추가해야함을 잊지 말자.
다시 역추적하여 현 위치는 $e Node$이다. 이미 $c, f Node$는 방문 한 상태이므로 $e Node$는 Terminal Node이다. 방문 표시 후 stack에서 빼내고 역추적하자. 반드시 지나 온 경로로 역추적 해야하기에 $b node$로 이동한다.

stack 내에 $c Node$가 존재하지만, 이미 방문했으므로 바로 stack에서 빼낸다. 남은 $b Node$를 stack에서 빼내고 방문처리하면 stack은 Empty이다. 아직 $a,d,g Node$를 방문하지 않았으므로 남은 Node 중 Random Choice를 하자.
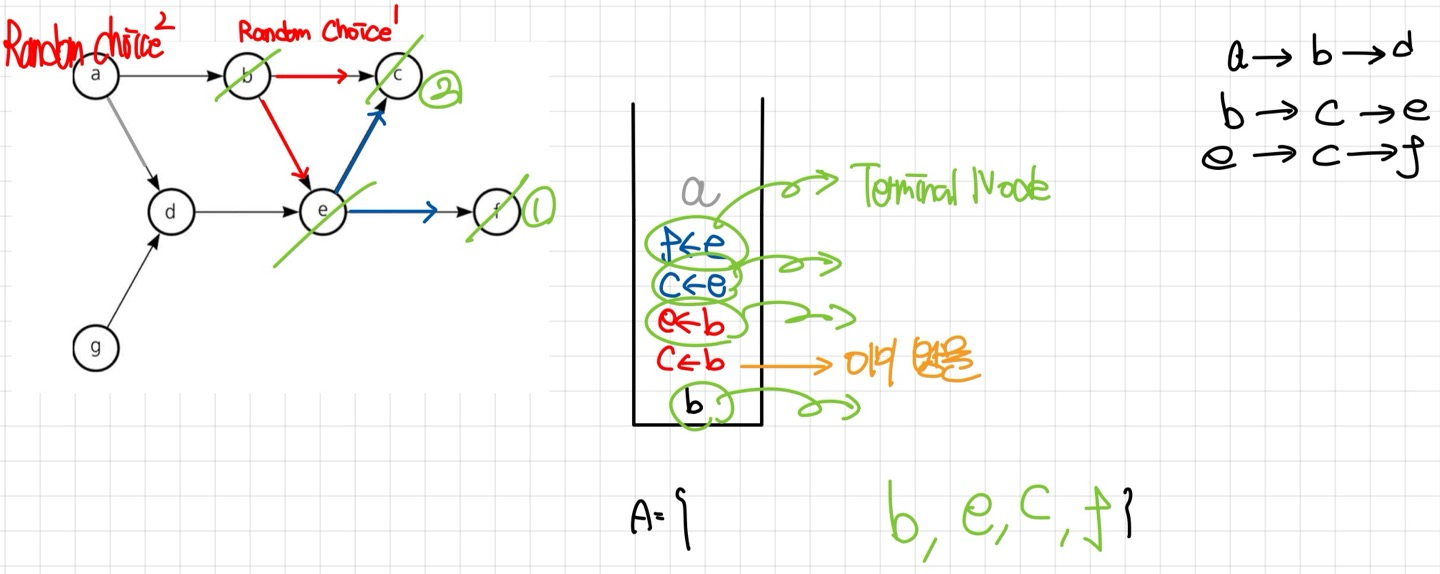
Random Choice 된 Node는 $a Node$이다. 이동할 수 있는 Node는 $d Node$뿐이므로, stack에 넣은 뒤 이동하자.
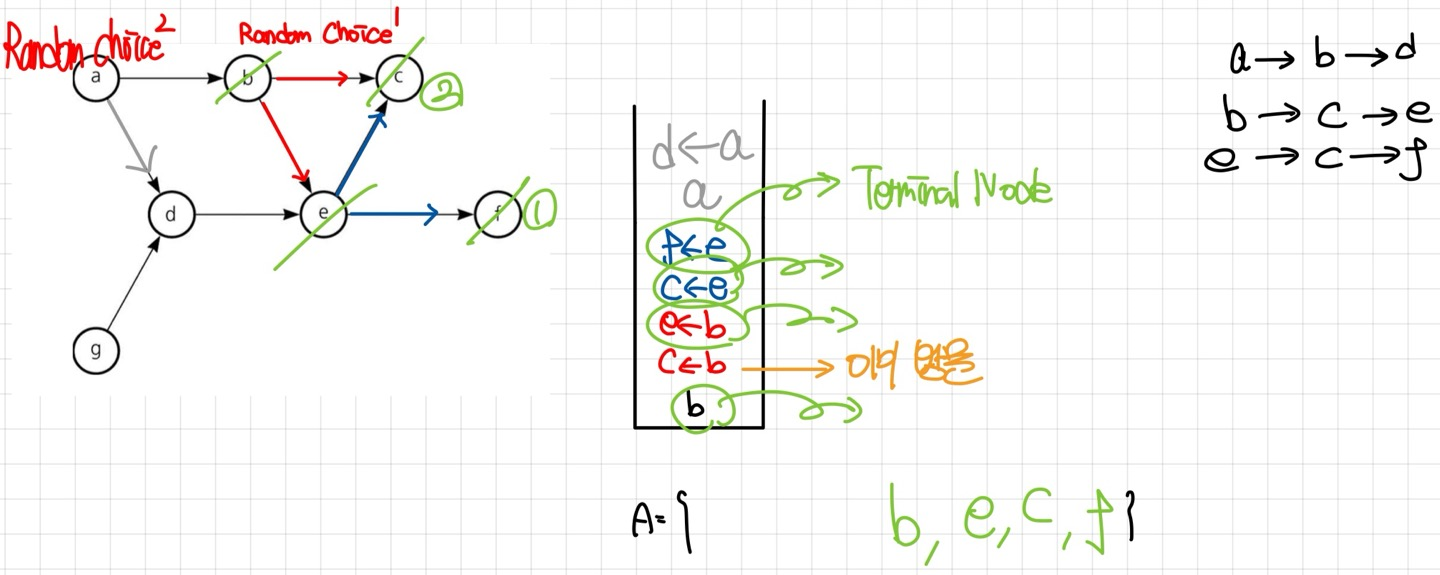
$d Node$는 이미 $e Node$를 방문 한 상태이므로 Terminal Node이다. 방문하고 stack에서 빼낸 뒤 역추적하자. 남은 $a Node$역시 Terminal Node이므로 방문하고 stack에서 빼내자.
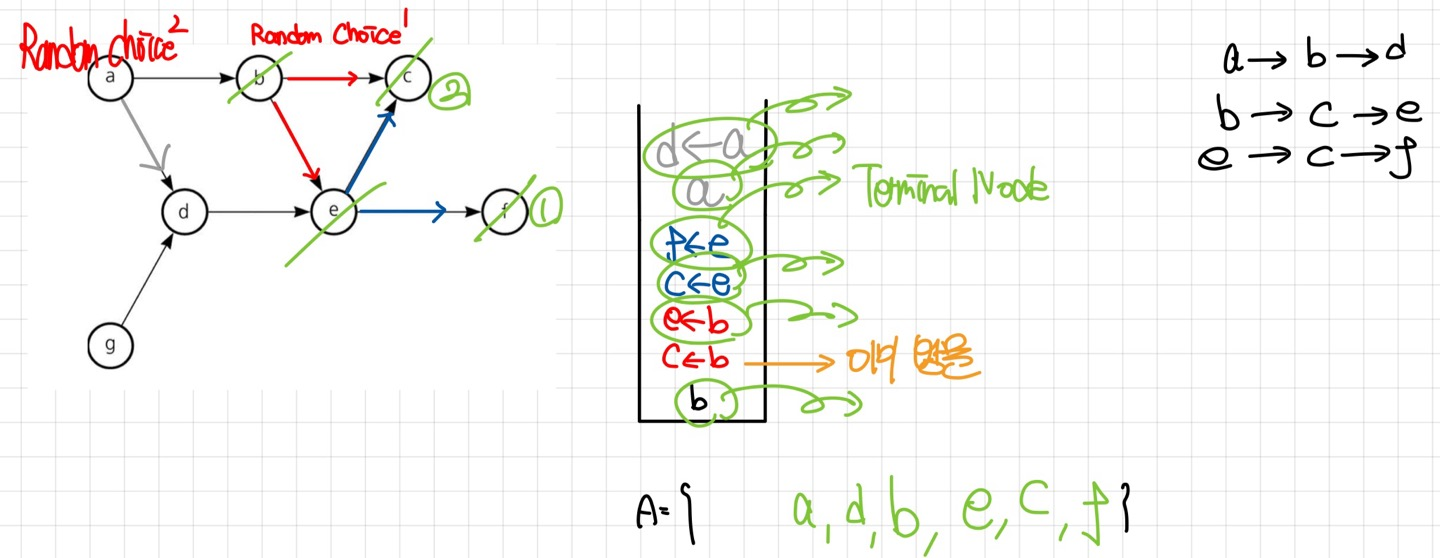
남은 Node는 $g Node$ 이므로 방문하자. 최종적인 $A$ Array는 다음과 같다.
$$ A = [g, a, d, b, e, c, f]$$
첫번째 Algorithm을 기반으로 비교 해 보면 잘 구했음을 확인할 수 있다.
두번째 Topological Sorting 알고리즘을 정리하자면, 모든 Node 중 Random Choice하여 해당 Node를 기준으로 Terminal Node까지 DFS를 수행한다. Terminal Node에 대해서만 방문한 뒤, 순서를 저장하는 배열의 앞부분에 추가하고 역추적한다. 역추적 과정에서 방문 가능한 다른 노드가 있다면 방문한다(DFS). 이 과정을 방문하지 않은 전체 노드에 대하여 반복적으로 수행하는 것이다.
직접 하나하나 해보면 이해가 쉬울 것이다.
'2024 > Study' 카테고리의 다른 글
| [ 영상 처리 ] Ch11. Computational Photography(2) (0) | 2024.06.08 |
|---|---|
| [ 영상 처리 ] Ch11. Computational Photography(1) (2) | 2024.06.05 |
| [ 영상 처리 ] Ch8. Clustering and Segmentation(3) (0) | 2024.06.01 |
| [ 영상 처리 ] Ch8. Clustering and Segmentation(2) (0) | 2024.06.01 |
| [ 영상 처리 ] Ch8. Clustering and Segmentation(1) (0) | 2024.05.29 |




