| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- DP
- MySQL
- 백준
- LSTM
- C++
- image processing
- 딥러닝
- opencv
- 그래프 이론
- CNN
- deep learning
- r-cnn
- machine learning
- RL
- UC Berkeley
- AlexNet
- GIT
- hm3d
- YoLO
- 강화학습
- CS285
- Reinforcement Learning
- NLP
- dynamic programming
- dfs
- BFS
- hm3dsem
- ubuntu
- 머신러닝
- Python
- Today
- Total
JINWOOJUNG
PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation 본문
PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation
Jinu_01 2025. 2. 3. 23:20Paper
Introduction
기존 Deep Learning 연구에서의 CNN은 Regular Input Data를 기반으로 동작한다(Image, Voxel, etc). 하지만, Point Cloud는 순서가 없는(Inordered) Inrregular Data이다. 따라서 Raw Point Cloud Data(PCD)를 CNN의 Input으로 취하는 것은 한계가 있다.
전처리 과정에서 PCD를 Regular Form(3D Voxel Grid, Collections of Images, etc)으로 변환하는 과정은 불필요한 메모리 및 계산 시간 증가를 초래하며, Quantization Artifacts에 의한 원본 정보 왜곡 및 Natural Invariances이 깨질 수 있다.
Quantization Artifacts는 연속적인 값을 Discrete 값으로 변환할 때 발생하는 정보의 손실과 왜곡을 의미한다.
PCD는 일반적으로 X, Y, Z Position Information을 포함하는데, (3.7482, 4.2314, 0.3271)의 정보를 Quantization을 통해 (3.5, 4.0, 0.0)과 같이 변형된다면 정보가 손실되고 왜곡된다. 이는 객체의 표면에 뿌려진 PCD가 가지는 Shape 정보를 왜곡시키는 등 Natural Invariance(자연적 불변성)을 깰 수 있다.
- Point Cloud
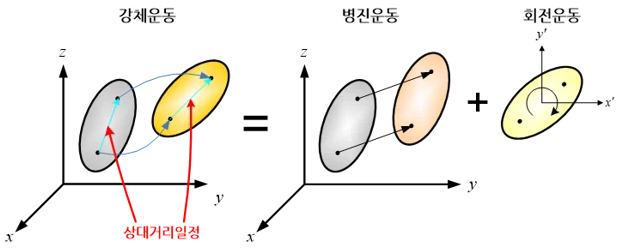
Point Cloud는 3차원 공간의 점들의 모음으로, Permutation Invariance를 가진다. 즉, 3D Points의 순서가 바뀌어도 동일한 객체를 의미하며, $n$개의 Points가 만들어 낼 수 있는 $n!$가지의 조합이 모두 동일한 결과를 나타낸다. 또한, Rigid Motion(강체 운동) Invariance를 가진다. Rigid Motion은 Translation + Rotation을 의미하며, 동일한 객체가 평행 이동 및 회전을 하여도 해당 객체에 대한 Point Cloud는 Point 사이의 상대적 거리와 구조를 유지하기 때문에 강건하다.
- Voxel
3D 공간을 작은 정육면체로 나눈 형태이다. Regular Form을 가지지만 Point Cloud에 비해 많은 메모리와 계산을 필요로 하며, 해상도가 증가할수록 기하급수적으로 늘어난다.
- Mesh
점, 선, 면으로 구성된 3D 표현 방식. 객체의 Shape을 삼각형으로 임의의 방식으로 연결하여 표현하기 때문에 동일한 객체여도 표현할 수 있는 수많은 방법이 존재한다(Combinatorial Irregularity, 조합적 불규칙성). 또한, Shape를 정밀하게 표현하기 위해서는 많은 삼각형으로 표현해야 하기 때문에 복잡하다(Complexity).

본 논문에서는 Input Data를 Point Cloud를 직접 활용하는 PointNet을 제안한다. PointNet은 연속적인 집합 함수를 근사할 수 있음을 증명하며, Input Point Cloud 중 Key Points로 요약(Feature)하여 학습함을 증명한다. 여기서 집합 함수란, Point Cloud를 처리하는 함수(Network)를 의미한다.
PointNet은 Shape Classification, Part Segmentation, Scene Segmentation Task의 Benchmark Dataset에 대하여 훨씬 빠르고 우수한 성능을 보인다.
Problem Statement
Deep Learning Network를 설계하기 이전, 기존 Image와 달리 3D PCD이기 때문에, PCD에 대한 정의와 각각의 Task가 의미하는 바를 정의 해 보자.
Point Cloud는 $ \left\{ P_i|i = 1, \cdots, n \right\}$로 정의되며, $P_i$는 Point의 위치 정보인 $(x,y,z)$를 가지는 Vector 형태이다.
- Object Classification
- Input
- 특정 객체에 대해 Random Sampling 된 Point Cloud
- Scene에서 객체에 대해 Segmeted 된 Point Cloud
- Output
- 모든 $k$ 개의 후보 클래스에 대한 Score
- Input
- Semantic Segmentation
- Input
- 하나의 객체에 대한 Point Cloud $\to$ Part Region Segmentation(부위별 세분화)
- 3D Scene의 Sub-volume $\to$ Object Region Segmentation(객체 영역 세분화)
- 3D 장면에서 특정 영역에 대해 해당 영역에 어떤 객체가 있는지
- Output
- $n \times m$ 점수 : $n$개의 각각의 Point가 $m$개의 Segmentation Category에 속하는 점수
- Input
왼쪽이 Part Region Segmentation, 오른쪽이 Object Region Segmentation의 결과이다.


Deep Learning on Points Sets

Properties of Point Sets in $\mathbb{R}^n$
PointNet의 Input Data인 Point Cloud의 특성을 다시 한번 살펴보자
- Unordered
Point Cloud는 Order(순서)가 없는 Point Set이다. 즉, $N$개의 3D Point Set에 대하여 가능한 $N!$가지의 Permutations(순열)에 Invriant 해야 한다.
- Interaction among Points
Points 들은 서로가 고립된 것이 아닌 공간적 거리를 통해 상호 연결되기에, 이웃하는 Points 간의 의미있는 subset을 형성한다. 따라서 Network는 이웃 Points로 부터 지역적 구조를 학습해야 하며, 지역 구조들 간의 Combinatorial Interactions(조합적 상호작용)을 학습할 수 있어야 한다.
- Invariance under Transformations
Point Cloud는 강체 변환에 불변해야 하며, 강체 변환으로 인한 Point Cloud의 Category, Segmentation의 결과가 변하면 안된다.
PointNet Architecture
Symmetry Function for Unordered Input
Point Cloud를 Input으로 하는 PointNet은 Input Permutation에 대하여 Invariant 해야 한다.
- 입력 데이터를 정렬(Sort)하여 표준적인 순서(Canonical Order)를 부여
가장 쉽게 떠오르는 방법은 Point Cloud를 표준적인 순서로 정렬하는 방법이다. 하지만, Point Cloud Data와 같이 3차원 혹은 고차원의 데이터에 대하여 약간의 Perturbations(변동)에 대해 안정적인 정렬 방법은 존재하지 않는다. 만약 정렬 방법이 존재한다고 하면, 3차원 공간에서 1차원 실수선으로 Bijection Map(1:1 Mapping)을 정의하는 것과 동일하다. 이때, 고차원에서의 공간적 근접성이 1차원 실수선으로 Mapping 된 후에도 유지되어야 하는데, 차원이 축소하는 과정에서 이를 유지하기 힘들다.
실제로 정렬 된 Input에 대하여 MLP를 적용하였을 때 약간의 성능 향상은 존재하나, 본 논문에서 제안하는 PointNet의 구조와 비교했을 때 성능이 저조해 근본적인 해결책이 될 수는 없다.
- 입력 데이터를 순차적으로 처리하도록 RNN을 학습
Point Cloud를 Sequence Data로써 처리하도록 RNN을 학습시키는 방법은 Point Cloud와 같이 수천~수십만 개의 Input에 대해서는 한계가 존재한다.
RNN 계열의 모델 중 하나인 LSTM으로 학습시킨 결과 역시 성능이 저조함을 확인할 수 있다.

- Symmetry Function(대칭 함수)
본 논문에서는 Symmetry Function으로 순열 불변성을 해결한다. Symmetry Function은 덧셈, 곱셈과 같이 입력 순서와 무관한 결과를 도출하는 함수를 의미한다. 아이디어는 Point Cloud에 대해 일반적으로 정의되는 함수 $f$를 집합 내 각각의 Point에 대해 변환 $h$를 적용한 뒤, 대칭 함수 $g$를 적용해서 근사하는 것이다.
여기서 일반 함수 $f$는 PointNet Network에서 Input Data Point Cloud를 처리하는 과정을 의미하며, 이를 $h, g$로 근사함을 의미한다.
이를 통해 Point Cloud의 순열에 불변하게 처리할 수 있음을 의미한다.
$$f\left (\left\{ x_1, \cdots, x_n\right\} \right ) \approx g\left ( h(x_1), \cdots, h(x_n) \right )$$
이때, $f : 2^{\mathbb{R}^N} \to \mathbb{R}^K$로, $\mathbb{R}^N$ 공간의 Point Cloud의 부분집합을 의미하며, $\mathbb{R}$는 PointNet의 Output을 의미한다. 즉, 우리가 근사하고자 하는 함수 $f$는 Point Cloud를 입력으로 받아 하나의 Scalar Value(Score)를 출력하는 함수를 의미하며, 이는 집합 함수를 학습하는 문제를 의미한다.
이를 근사하는 방법은 각각의 Point에 대해 적용되는 변환함수인 $h : \mathbb{R}^N \to \mathbb{R}^K$을 통해 $K$ 차원의 Feature를 출력하는 함수와 모든 점들의 특징을 합쳐 입력된 Point Cloud의 순서에 상관없이 같은 출력을 만들어 순열 불변성을 보장하는 대칭 함수인 $g : \mathbb{R}^K \times \cdots \times \mathbb{R}^K \to \mathbb{R}$의 조합으로 근사된다. 이때, PointNet에서 $h$는 MLP, $g$는 Single Variable Function과 Max Pooling의 조합으로 사용한다.
예를 들어, 3개의 Point를 가지는 Point Cloud $P = \left\{ (1.0, 2.0, 3.0), (2.0, 3.0, 9.0), (1.4, 2.4, 0.7) \right\}$라 하자. 각각에 대한 변환 함수를 적용한 결과가 $h(x_1) = (0.1, 0.5, 0.2), h(x_2) = (0.3, 0.5, 0.7), h(x_3) = (0.4, 0.9, 0.6)$이라고 한다면, $g(h(x_1), h(x_2), h(x_3)) = (max(0.1, 0.3, 0.4), max(0.5, 0.2, 0.9), max(0.2, 0.7, 0.6)) = (0.4, 0.9, 0.7)$
이러한 $h$의 집합을 통해, Point Cloud의 다양한 속성(Feature)를 학습할 수 있다.
Local and Global Information Aggregation

Classification Network를 통해 추출한 Global Feature를 바탕으로 SVM 혹은 Multi-layer Perceptron Classifier를 통해 Classification Task를 수행할 수 있다. 하지만, Point Segementation을 위해선 Local, Global Feature 모두가 필요하다.
본 논문에서는 $n \times 64$ 크기의 Per-point(Local) Feature와 Global Feature를 결합한 정보를 바탕으로 새로운 Per-point Feature를 추출하여 Segmentation Task를 수행한다.
Joint Alignment Network

특정 객체가 강체 변환을 거치더라도 강건성을 가지도록 Network는 학습되어야 한다.
본 논문에서는 Mini Network T-Net을 통해 Affine Transformation Matrix를 예측하고, 이를 각 Point에 적용한다. T-Net은 독립적인 Feautre Extraction, Max Pooling, FC Layer로 구성되며, PointNet과 유사한 구조를 가진다.
이는 각 Input Point에 대해서만이 아니라, Feautre Space로 확장하여 Feature를 표준적인 공간으로 정렬시키는 Feature Transformation Matrix($A$)를 예측하여 각 Feature에 적용한다. 하지만, 고차원인 Feature에 적용하기에는 최적화가 어렵기 때문에 Softmax Loss에 Regularization Term을 추가해서 특징 변환 행렬이 직교 행렬에 가깝도록 제약한다.
$$L_{reg} = \left\| I - AA^T\right\|^2_F$$
$AA^T = I$는 $A$가 직교행렬임을 의미하며, 직교 변환을 통해 입력 정보의 손실을 막을 수 있다.
Input Point Cloud, Feature에 대해 변환을 예측하는 과정은 결국 특정한 표준 공간(Cononical Space)로 변환하여 강체 변환에도 Invarient하도록 학습하기 위함이다.
이때, 변환행렬이 직교행렬이 되도록 Regularization Term을 추가하는데, 직교행렬은 모든 Column Vector가 자기 자신을 제외한 나머지 Column Vector와 직교이면서 크기가 1인 단위 벡터들로 구성된 행렬을 의미한다. 직교행렬 특징 상 직교 행렬을 변환 행렬로 적용한 뒤 거리와 각도의 변화가 없기 때문에, 해당 변환 행렬로 Input Point Cloud, Feature를 변환하면 강체 운동에 강건성을 학습할 수 있다.
Theoretical Analysis
Universal Approximation
PointNet은 Continuous Set Function(연속적인 집합 함수)에 대한 Universal Approximation Ability(보편 군사 능력)을 가짐을 주장한다. 즉, Point Cloud의 작은 변동(Perturbation)이 존재해도 Output(Classification, Segmentation Score)이 크게 바뀌지 않아야 함을 의미한다.
$$X = \left\{ S : S \subseteq [0, 1]^m \; and \; |S| = n \right\}, \qquad f : X \to \mathbb{R}$$
이때, 집합공간 $X$는 크기가 $n$인 집합 $S$들로 이뤄진 공간이며, $f$는 Hausdorff Distance $d_H$에 대해 연속적인 집합 함수 즉, 작은 변화에 대해 출력에 극심한 변화가 없음을 의미한다.
Hausdorff Distance란, 두 점 집합 사이의 거리를 측정하는 방법이다. 단순히 두 Point 간의 거리는 $L_2$ Distace 등으로 계산할 수 있지만, 점 집합 사이의 거리는 임의의 두 점으로 측정할 순 없다.

Hausdorff Distance는 $S, S"$에 대해서 각 점이 서로 가장 가까운 점 까지의 거리 중 최댓값을 의미한다. 따라서 $S, S'$이 하나라도 차이가 나면 $d_H(S, S')$이 커지게 되기 때문에, 두 점 집합의 유사도를 측정할 수 있다.
따라서, 본 논문에서는 "Point Cloud가 조금 변하면 즉, $d_H(S, S') < \delta$면, Network의 출력이 크게 달라지지 않아야 한다($|f(S) - f(S')| < \epsilon $)"는 의미에서 연속성이 보장되어야 한다고 언급한다. 이를 통해 약간의 작은 변동(Noise, Point 삭제/추가)에서 강건성을 보일 수 있다.
본 논문에서는 Max Pooling의 차원($K$)가 충분히 크면, PointNet이 임의의 연속적인 집합 함수를 학습할 수 있음 주장한다.
직관적으로 봐도 Max Pooling을 사용한다면 Point Cloud의 순서나 작은 변동에도 강건한 결과를 얻을 수 있다.

이때, $h$는 Feature Extraction Function(MLP), $MAX$는 Max Pooling, $\gamma$는 최종 출력 결정(MLP)를 의미하며 PointNet의 구조가 임의의 연속적인 집합 함수를 근사할 수 있음을 수학적으로 증명한다.
Bottleneck Dimension and Stability
Max Pooling Layer의 차원인 $K$에 영향을 받는다는 것을 발견하였다. 그렇다면, PointNet의 Stability와 모델의 정보 압축 특성의 측면에서 이를 살펴보자.

특정한 두 부분집합 $C_S, N_S$에 대해서, 두 부분집합 사이의 점들로 구성된 경우 신경망의 출력에 차이가 없음을 의미하며, 이때, $C_S$의 크기 즉, 중요한 점들의 개수는 $K$보다 크지 않음을 의미한다.
다시 정리하면, Network는 모든 Input Point Cloud가 아닌 특정한 $C_S$개를 포함하고 있다면 출력은 동일하며, 그 크기는 Max Pooling Layer의 차원 $K$보다 작다. 따라서 PointNet은 Input PCD에 작은 오류나 노이즈가 있어도 $C_S$를 포함하고 있으면은 Network의 출력이 크게 변하지 않고 강건함을 의미한다. 이때, $C_S$를 Critical Point Set of $S$라 부르며, $K$를 Bottleneck Dimension of $f$라 한다. 또한, PointNet은 Point Cloud를 Critical Point로 요약하는 법을 학습함을 의미한다.
Experiment
3D Object Classification

전통적인 Point Cloud Feature Extraction(점 밀도, D2 거리, Shape Contour, etc)을 사용한 MLP Model들과 비교한 결과 우수한 성능을 보인다. 여전히 멀티뷰 렌더링 기반인 MVCNN의 성능보다는 약간 낮은 수준인데, 이는 하나의 객체에 대한 여러 장의 이미지에서 얻을 수 있는 Feature(기하학적 특징)를 PointNet에서는 얻지 못하기 때문이다.
3D Object Part Segmentation

[27],[29]는 Point-wise Geometry Feature과 Correspondences between shapes(형상 간 대응)을 활용한 방법이다. PointNet이 전반적으로 우수한 성능을 보이지만, 일부 Class에 대해서는 낮은 정확도를 보인다.

PointNet의 강건성을 검증하기 위해서 Kinect Scan Data에 대해 6개의 무작위 시점에서 불완전한 Point Cloud를 생성하여 학습시킨 결과 평균 IoU가 5.3% 감소 하였지만, 정성적인 평가 결과 상당히 합리적으로 모델이 예측하였음을 확인할 수 있다.
Semantic Segmentation in Scenes

Hand-crafted Point Feature를 사용하는 baseline과 비교하였을 때 뛰어난 성능을 보인다.

Segmentation 한 결과를 시각화 한 결과 Point의 일부가 누락되거나 가려진 상황에서도 강건함을 확인할 수 있다.
'딥러닝 > 논문' 카테고리의 다른 글
| PointPillars: Fast Encoders for Object Detection from Point Clouds (0) | 2025.02.18 |
|---|---|
| VoxelNet: End-to-End Learning for Point Cloud Based 3D Object Detection (0) | 2025.02.05 |
| Focal Loss for Dense Object Detection(RetinaNet) (0) | 2025.01.22 |
| SSD: Single Shot MultiBox Detector (0) | 2025.01.20 |
| You Only Look Once: Unified, Real-Time Object Detection(YOLO) (0) | 2025.01.19 |




