| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- machine learning
- RL
- YoLO
- LSTM
- opencv
- r-cnn
- Python
- dfs
- CNN
- C++
- 그래프 이론
- 강화학습
- hm3dsem
- NLP
- ubuntu
- image processing
- deep learning
- UC Berkeley
- AlexNet
- hm3d
- GIT
- MySQL
- Reinforcement Learning
- 머신러닝
- CS285
- dynamic programming
- 백준
- BFS
- 딥러닝
- DP
- Today
- Total
JINWOOJUNG
[RL] CS285: Lecture 05. Policy gradients(1) 본문
본 포스팅은 UC Berkeley 에서 진행된 CS285: Deep Reinforcement Learning, Decision Making and Control
강의자료 및 강의를 기반으로 공부한 내용을 정리하는 포스팅입니다.
https://jinwoo-jung.tistory.com/174
[RL] CS285: Lecture 04. Introduction to Reinforcement Learning(2)
본 포스팅은 UC Berkeley 에서 진행된 CS285: Deep Reinforcement Learning, Decision Making and Control강의자료 및 강의를 기반으로 공부한 내용을 정리하는 포스팅입니다.https://jinwoo-jung.tistory.com/173 [RL] CS285: Lecture
jinwoo-jung.com
Policy gradients
Policy gradients는 Model free RL algorithm이다. 즉, $p(s_1), p(s_{t+1}|s_t,a_t)$를 Model을 통해 아는것이 아닌, Sample을 보고 상호작용 하는 것이다. 그리고 Expectation은 Samples의 평균으로 근사하여 학습에 활용된다.
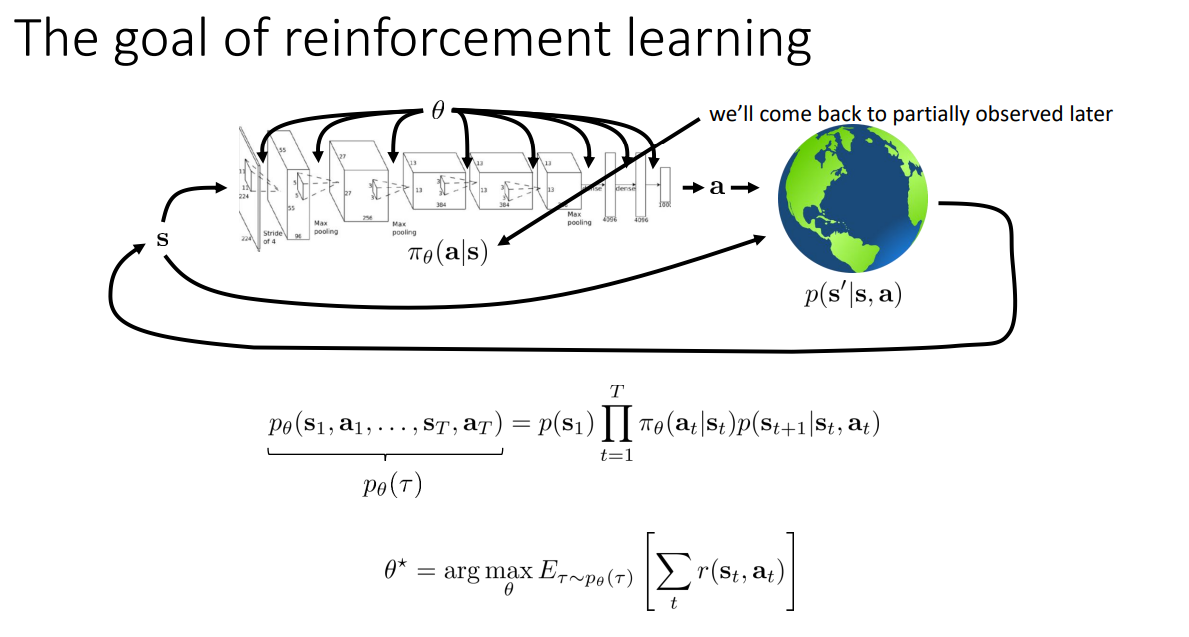
우리는 Reinforcement learning의 Objective function을 다음과 같이 정의할 수 있음을 이전 강의에서 살펴봤다. 이때, $J(\theta)$를 재정의하면 아래와 같으며 이는 정책 $\pi_\theta$의 기대 누적 보상(Objective)라 한다. 이때, 기대값은 분포를 알아야 정확히 계산 가능하지만 실제로 완벽히 알 수 없기 때문에, $\pi_\theta$를 실제로 실행해서 samples를 $N$개 뽑아 평균을 내어 근사한다.

조금더 수학적으로 살펴보자. Trajectory를 고려하면, Objective의 수식을 다음과 같이 쓸 수 있다.
$$J(\theta) = E_{\tau \sim p_\theta(\tau)}\left [\sum_{t=1}^{T}r(s_t,a_t) \right ] = E_{\tau \sim p_\theta(\tau)} \left [ r(\tau) \right ]$$
이후, Expectation의 정의를 이용하면 다음과 같이 변형 가능하다.
$$J(\theta) = E_{\tau \sim p_\theta(\tau)} \left [ r(\tau) \right ] = \int p_\theta(\tau)r(\tau)d\tau $$
그렇다면 Objective의 Gradient는 어떻게 될까?
$$\nabla_\theta J(\theta) = \int \nabla_\theta p_\theta(\tau)r(\tau)d\tau$$
이때, Convenient identity라는 간단한 Trick을 이용하면 식을 간단히 정리할 수 있다.
$$\frac{d}{d\theta}logf(\theta) = \frac{1}{f(\theta)}\frac{df(\theta)}{d\theta}$$
$$p_\theta(\tau)\nabla_\theta log p_\theta(\tau)=p_\theta (\tau)\frac{\nabla_\theta p_\theta(\tau)}{p_\theta (\tau)} = \nabla_\theta p_\theta(\tau)$$
따라서 Gradient 식을 다시 전개하면,
$$ \int \nabla_\theta p_\theta(\tau)r(\tau)d\tau = \int p_\theta(\tau) \nabla_\theta log p_\theta(\tau)r(\tau)d\tau = E_{\tau \sim p_\theta(\tau)} \left [ \nabla_\theta log p_\theta(\tau)r(\tau) \right ]$$

Objective의 Gradient를 조금 더 정리 해 보자.
Expectation 안에 $log p_\theta(\tau)$ Term을 분해 해 보면, 오른쪽 상단과 같이 분해할 수 있다. 이를 Gradient 안에 넣으면 $\theta$를 포함하지 않는 부분은 미분시 날라가므로 최종적으로 다음과 같이 정리할 수 있다.
$$\nabla_\theta J(\theta) = E_{\tau \sim p_\theta(\tau)} \left [ \left ( \sum_{t=1}^{T} \nabla_\theta log \pi_\theta(a_t|s_t) \right )\left ( \sum_{t=1}^{T} r(s_t,a_t) \right ) \right ]$$

기대값으로 정의된 Objective $J(\theta)$와 그 Gradient는 직접 계산이 어려우므로, $\pi_theta$를 $N$번 실행해 얻은 Trajectory samples의 평균으로 Monte Carlo 근사하면 아래와 같다. 이렇게 얻은 Gradient 추정치는 unbiased하며, 이를 사용해 Gradient ascent로 $J(\theta)$를 최대화하도록 $\theta$를 업데이트 할 수 있다.
$E[\hat{\mu}] = \mu$ 일 때, unbiased라고 한다. 이는 분산은 크지만 기대적으로는 참값을 정확히 추정함을 의미한다.
우리는 Convenient identity를 통해 Gradient를 기대값 형태로 표현할 수 있었고, 그 기대값을 동일한 분포에서 샘플링한 Trajectories의 Monte Carlo 평균으로 근사했기 때문에 unbiased 이다.
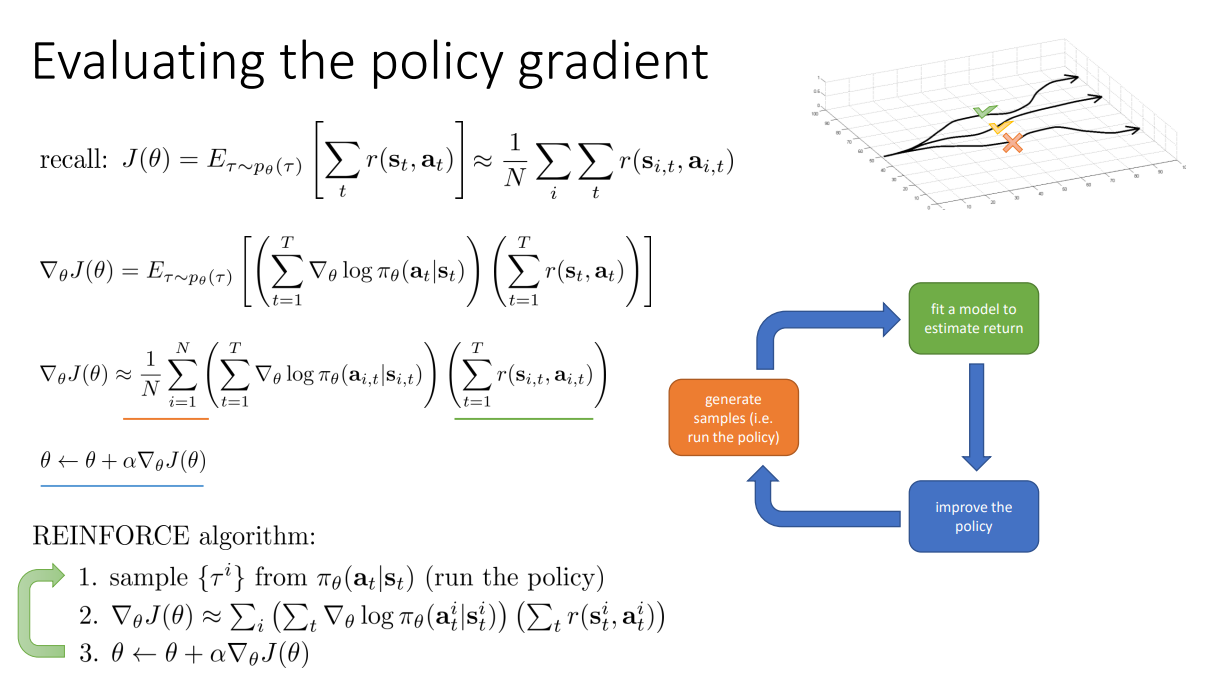
Understanding Policy gradients
Full observability
앞서 공부한 내용들을 다시 살펴보자. Objective와 Gradient of objective의 정의 및 실제로 Expectation 대신 $N$개의 Samples를 통해 평균내서 근사하는 방법을 살펴보았다.

그렇다면 Objective function의 Gradient가 의미하는 것은 무엇일까?
앞쪽 $\sum_{t=1}^{T} \nabla_\theta log \pi_\theta (a_{i,t}|s_{i,t})$ Term은 Trajectory에서 선택된 Actions가 Previous policy에 의해 얼마나 강하게 선택되었는지를 의미한다. 하지만 이 항 자체만으로 행동의 좋고 나쁨을 판단할 수 없다.
$\sum_{t=1}^{T} r(s_{i,t},a_{i,t})$ Term은 그 행동에 대한 결과로, 일종의 Weight로써 행동의 결과를 통해 학습의 방향을 조절하는데 활용된다. 즉, 이 Return term을 통해 좋은 행동(Return이 크다)의 확률이 커지도록 학습할 수 있는 것이다.
$$\nabla_\theta J(\theta) \approx \frac{1}{N}\sum_{i=1}^{N}\left ( \sum_{t=1}^{T} \nabla_\theta log \pi_\theta (a_{i,t}|s_{i,t})\right ) \left ( \sum_{t=1}^{T} r(s_{i,t},a_{i,t})\right ) $$
Maximum likelihood는 아래와 같이 정의되는데, Objective function와의 차이점은 Return term의 유무이다. 이는 Maximum likelihood에서는 모든 행동을 동일하게 취급하기에, Trajectory 상의 행동이면 무조건 더 자주 나오게 학습하기 때문이다.
$$\nabla_\theta J_{ML}(\theta) \approx \frac{1}{N}\sum_{i=1}^{N} \left ( \sum_{t=1}^{T} \nabla_\theta log \pi_\theta (a_{i,t}|s_{i,t}) \right ) $$
Partial observability
그렇다면 $s_t$가 아닌 $o_t$라면 달라질까? 더이상 Markov property가 사용되지는 않지만, 결국 식을 전개해 보면 $s_t$와 동일함을 확인할 수 있다.

What is wrong with the policy gradient?
RL은 그렇다면 이것만으로 잘 동작할까? 절대 아니다.
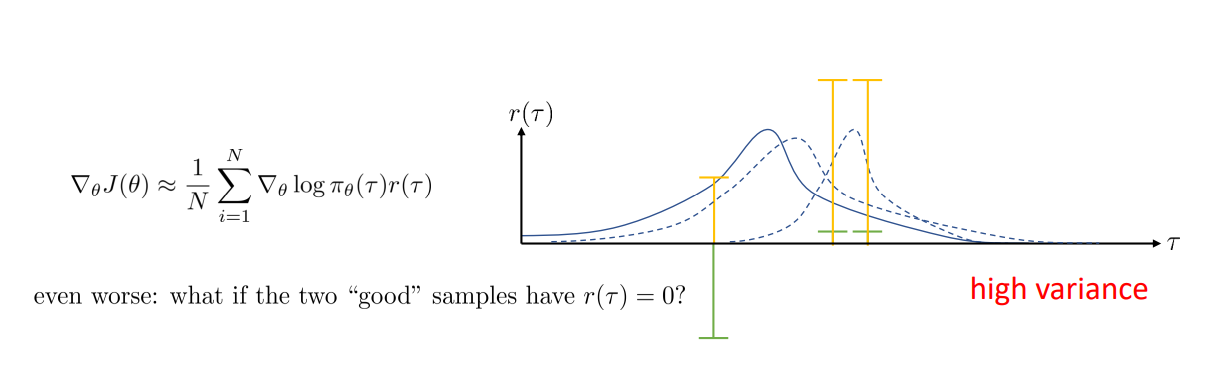
만약 Reward가 초록색으로 주어진다면, Policy gradient를 적용하면 Probability distribution이 양수인 Reward에서 증가하도록 학습되기에 오른쪽으로 크게 움직일 것이다.
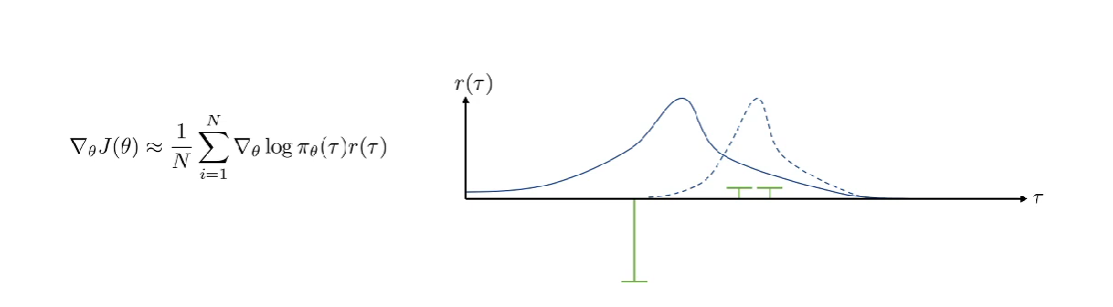
하지만 Reward가 모두 양수라면? 초록색 Reward와는 달리 급격한 변동은 줄어들 것이다.
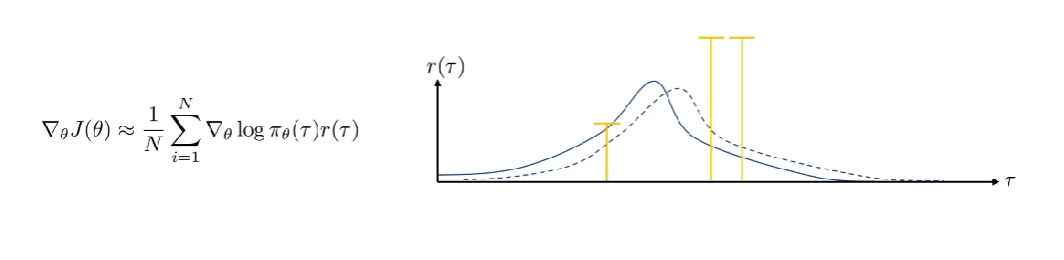
만약 오른쪽 두 양수의 Reward가 모두 0이라면? 왼쪽 Trajectory의 확률만 급격하게 줄이는 방향으로 변할 것이다. 이처럼 우리는 유한한 환경에서 Samples를 사용하기 때문에, 일정하지 못하고 High variance를 가지게 된다면 제데로된 학습을 할 수 없을 것이다.
Reducing Variance
그렇다면 이제 Variance를 줄일 수 있는 방법을 살펴보자.
Causality
Causality는 $t < t'$ 일 때, $t'$에서의 Policy는 $t$에서의 Reward에 영향을 주지 못함을 의미한다. 즉, 미래는 과거에 영향을 주지 못함을 의미한다. Gradient of objective function의 정의를 살펴보면, Reward term에서는 $ \sum_{t'=1}$ 을 고려하는데, 이는 과거/현재/미래의 Reward를 모두 고려함을 의미한다.
$$\nabla_\theta J(\theta) \approx \frac{1}{N}\sum_{i=1}^{N} \sum_{t=1}^{T} \nabla_\theta log \pi_\theta (a_{i,t}|s_{i,t}) \left ( \sum_{t'=1}^{T} r(s_{i,t'},a_{i,t'})\right ) $$
따라서 해당 항을 삭제하면 다음과 같이 재정의할 수 있다. 이때, $\sum_{t'=t}^{T} r(s_{i,t'},a_{i,t'})$ Term을 "reward to go"라고 칭하며, $\hat{Q_{i,t}}$라 표현한다.
$$\nabla_\theta J(\theta) \approx \frac{1}{N}\sum_{i=1}^{N} \sum_{t=1}^{T} \nabla_\theta log \pi_\theta (a_{i,t}|s_{i,t}) \left ( \sum_{t'=t}^{T} r(s_{i,t'},a_{i,t'})\right ) $$
그렇다면 단순히 $t' < t$ 부분을 삭제한다고 Variance를 줄일 수 있을까? 실제 계산은 생략하겠지만, $\nabla_\theta log \pi_\theta (a_t|s_t)r(s_t',a_t') , t' < t$의 Expectation을 계산해 보면 0이 나온다. 즉, 평균이 0인 값(Noise)을 제거함으로써 전체식의 평균은 변화가 없지만 Variance가 낮아짐을 의미한다.
Baseline
또 다른 방법은 Baseline을 활용하는 방법이다. 앞서 본 상황 중 Reward가 전부 양수인 경우도 있었다. 이처럼 단순히 Reward를 곱하는 것이 아닌 Reward에서 Baseline을 뺀 값을 곲해주는 방법인데, Policy gradients는 Rewards가 Centered일 때 동작하기 때문이다. 일반적으로 Baseline은 Reward의 평균을 활용한다.

그렇다면 실제로 잘 동작할까? 이 역시 계산해 보면 평균이 0임을 확인할 수 있다.
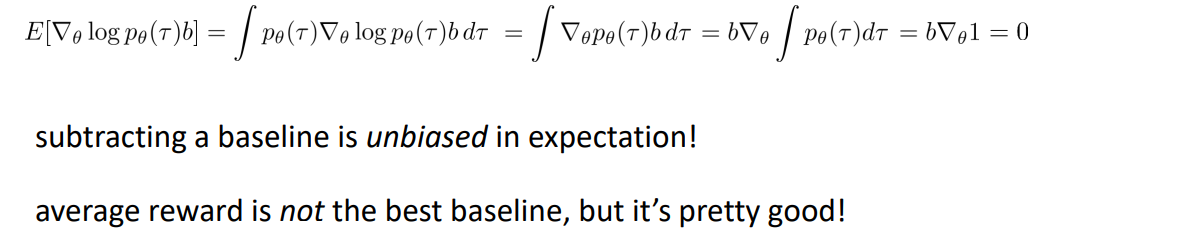
보통 평균을 사용하긴 하지만 이것은 최적의 Baseline이 아니다. 그렇다면 최적의 Baseline은 어떻게 구할까? Varaince와 Expectation의 관계식에 의해 구할 수 있다.
$$ Var[x] = E[x^2] - E[x]^2$$
우리가 원하는 Expectation은 다음과 같다.
$$E_{\tau \sim p_\theta(\tau)} \left [ \nabla_\theta log p_\theta (\tau) \left (r(\tau) - b\right)\right]$$
따라서 Variance를 전개해 보면 아래와 같다. 이때, Baseline의 Expectation은 unbiased이므로, 아래와 같이 간략화 할 수 있다.

이를 Baseline에 대해서 미분하면 아래와 같이 최적의 Baseline을 구할 수 있다. 조금 해석 해 보면, 최적의 Baseline은 Gradient magnitudes로 Weighted 된 Expected reward임을 확인할 수 있다. 하지만, 실제로 매 Update마다 이를 계산하려면 복잡하기에 잘 쓰이진 않지만, 아이디어는 많이 활용된다.

'Reinforcement Learning' 카테고리의 다른 글
| [RL] CS285: Lecture 06. Actor-Critic Algorithms(1) (0) | 2026.01.29 |
|---|---|
| [RL] CS285: Lecture 05. Policy gradients(2) (0) | 2026.01.28 |
| [RL] CS285: Lecture 04. Introduction to Reinforcement Learning(2) (0) | 2026.01.27 |
| [RL] CS285: Lecture 04. Introduction to Reinforcement Learning(1) (0) | 2026.01.27 |
| [RL] CS285: Lecture 02. Supervised Learning of Behaviors(2) (0) | 2025.12.14 |




