| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- CNN
- C++
- 머신러닝
- ubuntu
- 그래프 이론
- 강화학습
- image processing
- RL
- 딥러닝
- GIT
- BFS
- deep learning
- LSTM
- Python
- hm3d
- YoLO
- r-cnn
- MySQL
- dfs
- dynamic programming
- NLP
- 백준
- opencv
- UC Berkeley
- DP
- Reinforcement Learning
- AlexNet
- CS285
- hm3dsem
- machine learning
- Today
- Total
JINWOOJUNG
[RL] CS285: Lecture 04. Introduction to Reinforcement Learning(1) 본문
[RL] CS285: Lecture 04. Introduction to Reinforcement Learning(1)
Jinu_01 2026. 1. 27. 11:47본 포스팅은 UC Berkeley 에서 진행된 CS285: Deep Reinforcement Learning, Decision Making and Control
강의자료 및 강의를 기반으로 공부한 내용을 정리하는 포스팅입니다.
https://jinwoo-jung.tistory.com/170
[RL] CS285: Lecture 02. Supervised Learning of Behaviors(2)
본 포스팅은 UC Berkeley 에서 진행된 CS285: Deep Reinforcement Learning, Decision Making and Control강의자료 및 강의를 기반으로 공부한 내용을 정리하는 포스팅입니다.앞선 내용과 이어지는 포스팅입니다. 꼭
jinwoo-jung.com
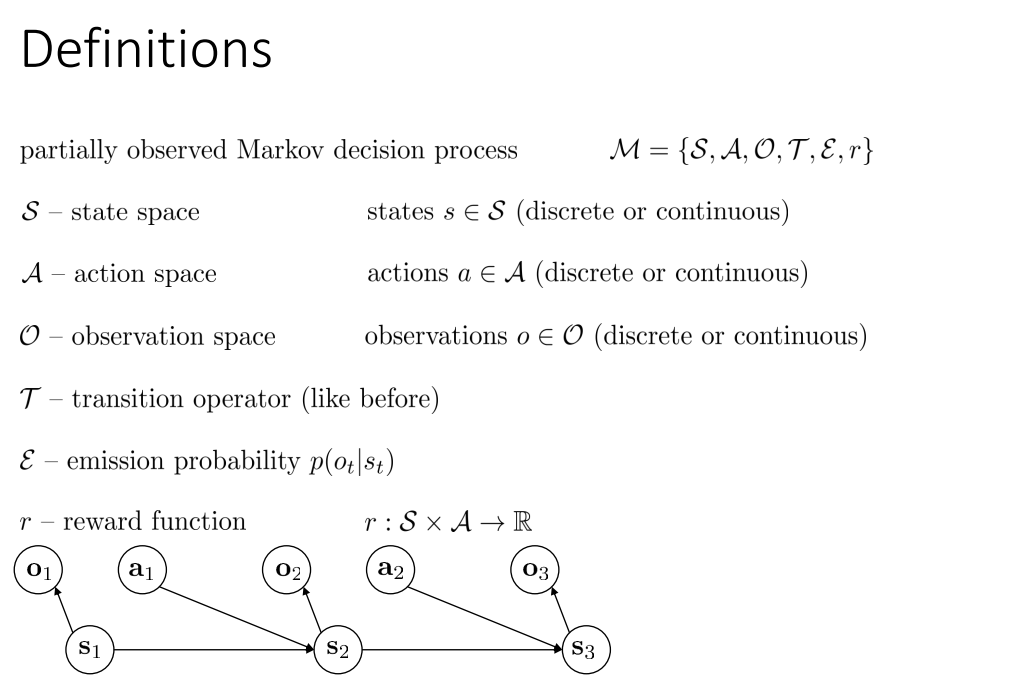
Definitions
몇가지 annotation에 대한 정의를 다시 한번 살펴보자.
아래 MDP에서 $s_1$에서 $s_2$로의 이동이 Transition probability(전이 확률)로 표현됨을 확인할 수 있다. 해당 모델은 Markov property를 가정하므로, $s_{t-1}$에 무관하게 현재 상태가 미래 상태를 결정하는데 충분하다.
지난 강의에서도 강조한 것 처럼, Observation $o_t$와 State $s_t$는 항상 다름을 유의하자. 예를 들어, 차량의 전방 카메라 영상이 Observation이라면, 차량의 속도, 방향, 위치 등의 모든 상태 값이 State이다.

앞선 강의에서 살펴본 Imitation learning(모방 학습)에서는 Ground truth 역할을 하는 Expert가 존재하였다. 따라서 Agent는 Expert와 동일하게 행동하도록 학습하면 되지만, 강화학습에서는 따로 Expert가 존재하지 않는다.
따라서 강화학습에서는 학습시킬 방향 즉, Policy가 달성해야 하는 목표를 정의해 주는 것이 필요한데, 이것이 바로 Reward functions(보상 함수)이다. $r(s, a)$로 표현되는 보상 함수는 어떠한 state, action이 더 좋은지를 의미하게 된다. 이때, 고민해야 할 점은 어떻게 나중에 더 좋은 보상을 가져올 행동을 지금 선택해야 할까? 이다.

Markov chain에 사용되는 용어들의 정의를 조금 더 살펴보자.
Markov chain은 Markov property를 만족하기 때문에, Transition operator $\mathcal{T}$는 $t$시점에서 $t+1$시점으로 State가 $s_t = j$에서 $s_{t+1}=i$로 이동하는 State transition operator(matrix)를 정의할 수 있다. 따라서 Markov chain $\mathcal{M}$은 State space $\mathcal{S}$, Transition operator $\mathcal{T}$로 구성된다. 이때, Transition operator가 operator인 이유는 $\mu_{t, i}$는 time $t$에서 state가 $i$에 있을 확률이므로 하나의 확률 벡터이고, $\mathcal{T}_{i,j}$는 $j$ state에서 $i$ state로 전이되는 확률로 구성된 Matrix이므로, $\vec{\mu_{t+1}} = \mathcal{T} \vec{\mu{t}}$는 상태를 전시키는 선형 변환의 operator로 동작하기 때문이다.

아래의 예시를 통해 실제 동작화는 과정을 이해 해 보자

Markov chain에서 Action이 포함된 경우를 Markov decision process(MDP)라고 한다. 이때, MDP는 Action space $\mathcal{A}$와 Reward $r$를 포함한다.


만약 완벽한 State가 아닌 Obesrvation을 가지는 경우 Partially observed MDP로 정의된다.
The goal of reinforcement learning
Markov property에 의해 일련의 Trajectory에 대한 Property는 아래와 같이 정의할 수 있다. State가 주어지면 Policy에 의해 Action이 선택되고, 그에 의한 전이 확률의 곱으로 정의됨을 확인할 수 있다.

그리고 Reinforcement learning의 Goal은 Trajectory 상에서 Agent가 얻는 Reward의 합이 최대가 되도록 하는 것입니다. Trajectory는 결국 Policy에 의해 선택되는 Action에 따라 달라지므로, Policy를 Parameter $\Phi$로 매개화되며, 앞으로 Policy로 Neural Network를 사용하면서 강의가 전개되므로 Weight라고 생각하면 된다.
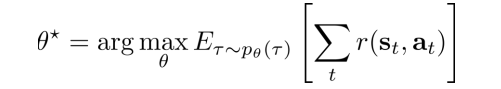
Finite horizon case: state-action marginal
$T$가 유한한 경우 Expectation의 특징을 살려 식을 아래와 같이 전개할 수 있습니다.

Infinite horizon case: stationary distribution
만약 $T$가 무한대라고 하면, Reward가 단순히 양수이면 무한대가 되어버려 수렴하지 않게 된다. 따라서 이런 경우 Stationary distribution을 가정하게 되는데, 이는 trainsition이 반복하게 진행되면 상태 분포가 더이상 변화되지 않고 유지됨을 의미한다. 따라서 $\mu = \mathcal{T} \mu$가 되고, 식을 변형하면 $(\mathcal{T}-\mathcal{I})\mu = 0$이 된다. 이는 선형대수적 관점에서 $\mu$는 eigen value가 1인 $\mathcal{T}$의 eigen vector임을 의미한다. 그리고 이러한 전개는 Ergodicitiy 즉, State는 어떠한 다른 State로도 0이 아닌 확률로 전이할 수 있음을 가정한 상태에서 유의미하다.

따라서 Infinite의 경우 다음과 같이 식이 전개된다. 어짜피 시간에 따라 변하지 않기 때문에 모든 값이 동일하여 $T$ Term이 상쇄된다.

그렇다면 강화확습에서는 왜 Expectation(기댓값)을 활용할까? 아래 예시처럼 Reward function $r(x)$는 불연속적이고, Action은 $\pi$라는 확률에 의해 결정된다고 하자. 그렇다면 Reward는 불연속적이지만, Reward의 Expectation은 연속적이다. 따라서 이는 Policy gradient에 사용할 수 있기 때문에 Expectation을 활용하게 된다.

Algorithms
강화학습의 동작 과정을 살펴보자.
강화학습은 Trial and error를 통해 학습하기 때문에 Generate samples 단계에서는 먼저 Samples를 생성하기 위해 Environment와 상호작용한다. Fit a model/estimate the return 단계는 Policy를 강화하기 위해 Return을 계산하는 단계이다. 마지막으로 Improve the policy 단계는 Policy를 더 좋은 방향으로 향상시키는 단계이다.

오른쪽 상단의 예시처럼 3개의 Samples가 생성되면, 각각의 Sample에 대해서 Total reward를 계산하고, 그에 따라 Policy gradient algorithms를 기반으로 좋은 Sample이 More likely 되도록 학습하게 된다.

Value Functions
지금부터는 수학적 지식이 조금 요구됨으로 천천히 따라가보자.
결국 강화학습의 목적은 Expectation of tatal reward를 최대로하는 것이다.

우리가 아는 수학적 지식을 적용하면, 아래 전개는 자명하다.
$$E_{X, Y}[f(X,Y)]=E_X[E_{Y|X}[F(X,Y)]]$$
따라서 이를 Expectation 전개식에 일부 적용 해 보면,
$$E_{s_1,a_1}[r(s_1,a_1)] = E_{s_1 \sim p(s_1)}[E_{a_1 \sim \Pi_\Theta(a_1|s_1)}[r(s_1,a_1)]]$$
$$E_{s_2,a_2}[r(s_2,a_2)] = E_{s_1}[E_{a_1|s_1}[E_{s_2|s_1,a_1}[E_{a_2|s_2}[r(s_2,a_2)]]]]$$
따라서 Expectation을 Recursive하게 표현하면 다음과 같다.
여기서 새로운 $Q$ function의 정의가 등장하는데, $Q(s_t, a_t)$은 time $t$의 $s_t$에서 $a_t$을 했을 때, 앞으로 받을 모든 reward의 기댓값을 의미한다.

따라서 우리는 Expectation of total reward를 Q function을 이용해 재정의할 수 있다.

그리고 Value function $V$를 정의할 수 있는데, 이는 time $t$의 $s_t$에서 앞으로 얻게될 reward의 기댓값을 의미한다. 따라서 Value function을 이용해서 Expectation of total reward를 재정의할 수 있고, 이는 RL의 Goal이 된다.

그렇다면 Q-function과 Value function을 이용해서 무엇을 할 수 있을까?
만약 우리가 Policy $\Pi$와 Q-function $Q^\pi (s,a)$를 알고 있다면, Q-function을 최대로 하는 action $a$에 대한 $\pi^\prime$를 1로 하면 $\pi^\prime$는 $\pi$보다는 좋은 Policy가 되기 때문에 Policy를 향상시킬 수 있다. 이것이 추후 Policy iteration algorithms로 이어진다.

다음으로는 Policy graident와 연결시킬 수 있다. 만약 $Q^\pi (s,a)$가 $V^\pi(s)$보다 크면, $a$가 평균보다 좋다는 의미이므로, $\pi$가 $a$를 선택할 확률을 증가하도록 학습하면 된다.

'Reinforcement Learning' 카테고리의 다른 글
| [RL] CS285: Lecture 05. Policy gradients(1) (0) | 2026.01.28 |
|---|---|
| [RL] CS285: Lecture 04. Introduction to Reinforcement Learning(2) (0) | 2026.01.27 |
| [RL] CS285: Lecture 02. Supervised Learning of Behaviors(2) (0) | 2025.12.14 |
| [RL] CS285: Lecture 02. Supervised Learning of Behaviors(1) (0) | 2025.12.14 |
| [RL] CS285: Lecture 01. Introduction (0) | 2025.12.08 |




