| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- hm3d
- hm3dsem
- GIT
- opencv
- DP
- deep learning
- C++
- 그래프 이론
- CNN
- BFS
- AlexNet
- machine learning
- UC Berkeley
- image processing
- CS285
- 머신러닝
- NLP
- YoLO
- Python
- RL
- LSTM
- r-cnn
- 백준
- dfs
- 강화학습
- dynamic programming
- MySQL
- Reinforcement Learning
- 딥러닝
- ubuntu
- Today
- Total
JINWOOJUNG
[RL] CS285: Lecture 02. Supervised Learning of Behaviors(1) 본문
[RL] CS285: Lecture 02. Supervised Learning of Behaviors(1)
Jinu_01 2025. 12. 14. 16:37본 포스팅은 UC Berkeley 에서 진행된 CS285: Deep Reinforcement Learning, Decision Making and Control
강의자료 및 강의를 기반으로 공부한 내용을 정리하는 포스팅입니다.
https://jinwoo-jung.tistory.com/168
[RL] CS285: Lecture 01. Introduction
본 포스팅은 UC Berkeley 에서 진행된 CS285: Deep Reinforcement Learning, Decision Making and Control 강의자료 및 강의를 기반으로 공부한 내용을 정리하는 포스팅입니다.Introduction다음과 같은 Robot이 있다고 가정
jinwoo-jung.com
Terminology & Notation
강화학습에 기본적으로 사용되는 용어를 정의해보자.
$s_t$는 state로, observation을 위한 모든 정보를 포함하는 environment의 현재 상태에 대한 모든 정보를 의미한다. $o_t$는 observation으로, state의 일부 정보를 포함하는 state의 부분집합이다. 아래 예시를 보면, observation은 치타가 영양을 사냥하는 장면을 의미한다. 하지만, state는 장면 뿐만 아니라 치타, 영양의 속도, 운동 방향, 환경 상태 등 물리학적으로 environment를 설명할 수 있는 모든 정보를 포함하는 값이다.

다음과 같이 차량이 치타를 가리고 있으면, $o_t$로는 치타가 사냥을 하고 있는지 정지하는지 어떤 상태인지 알 수 없다. 단순히 관측한 값(이미지)여서 그렇다. 하지만, $s_t$는 모든 정보를 포함하기에 알 수 있다.

다음으로 $a_t$는 action으로, agent의 동작(action)을 의미한다. 그리고 $a_t$는 $\pi_\theta(a_t|o_t)$에 의해 결정되는데, $\pi_\theta$란 policy로, agent가 어떤 action을 취할지 선택하는 정책을 의미한다.
따라서 아래 Probabilistic Graphical Models(PGMs: 확률적 그래픽 모델)과 같은 프로세스로 동작함을 확인할 수 있다. $s_{t+1}$는 $s_t$와 $\pi_\theta$에 의해 결정된 $a_t$에 의해 결정됨을 확인할 수 있다.
이때, Markov property란 현재 상태가 미래를 결정하는 데 충분하며, 과거 상태는 영향을 미치지 않음을 의미한다. 즉, 과거 History를 모두 고려하지 않기에 모델이 단순해질 수 있다. $s_{t+1}$이 예측되는 과정을 살펴보면 이해할 수 있다.

Imitation Learning
강화학습을 본격적으로 살펴보기 이전, Imitation Learning(모방학습) 중 하나인 Behavioral Cloning(BC, 행동 모방)에 대해서 먼저 살펴보자. 모방 학습이란 전문가(Expert)가 한 시연(Demonstration)을 Supervised Learning 문제로 바꿔서 학습하는 과정이다.
아래 예시를 보면, 운전자(전문가)가 우전하는 과정을 입력($o_t$)과 출력($a_t$)로 라벨링하여 학습 데이터로 만든 뒤, Supervised Learning 문제로 $\pi_\theta({a_t|o_t})$를 학습하여 이를 실제 Test 환경에서 관측한 $o_t$를 바탕으로 수행할 $a_t$를 결정하는 과정이다.

하지만, 실제로 BC를 적용하면 제데로 동작하지 않는다. 학습된 $\pi_\theta$기반으로 action을 수행한 trajectory를 보면 처음에는 잘 따라가다가 small mistake가 발생한 뒤로 trajectory를 벗어나더니 나중에는 big error로 이어짐을 확인할 수 있다.
왜 그럴까? 기존의 Supervised Learning에서는 IID property를 가지고 있다고 하였다. 즉, 각각의 training point가 다른 training point에 영향을 미치지 않음을 의미한다. 하지만, 강화 학습에서는 작은 실수가 발생한 $s_t$에서의 $a_t$가 $s_{t+1}$에 영향을 주기 때문에 $o_{t+1}$이 달라지기게 된다.

그러면 BC는 절대 잘 동작하지 않을까? 그건 또 아니다. NVIDIA에서 발표한 연구 중 하나는 Fake observation으로 이를 해결했는데, 단순히 전방 카메라 이미지 뿐만 아니라 왼쪽 카메라는 "turn right", 오른쪽 카메라는 "turn left"로 라벨링 하였다. 이를 통해 trajectory에서 벗어나는 action이 있어도 "turn right/turn left"로 라벨링 된 데이터에서 본 상태이기 때문에 recover이 가능하다.

이처럼 Naive BC를 해결하기 위한 여러 아이디어가 있는데 이를 하나하나 살펴보자

The distributional shift problem
먼저 BC가 잘 동작할 수 없는 요인을 수학적으로 살펴보자.
test 과정에서는 $p_{data}(o_t)$(observation 분포) 아래 학습된다. 하지만, 실제로 test 과정에서는 학습된 $\pi_\theta$를 기반으로 동작하기에 $p_{\pi_\theta}(o_t)$ 아래 동작한다. 따라서 trian과 test의 확률분포가 달라지는 $p_{data}(o_t) \neq p_{\pi_\theta}(o_t)$ 현상 때문에 BC가 정확히 동작할 수 없으며, 이를 Distributional Shift라 한다.

그렇다면 결국 BC가 잘 동작하기 위해서 우리의 목표(Goal)는 무엇일까?
단순히 $$ \underset{\theta}{max}E_{o_t \sim p_{data}(o_t)}\left [ log\pi_\theta(a_t|o_t)) \right ]$$ 가 목표면은 않된다. 앞서 본 예제처럼 우리는 보지 못한 환경에서도 좋은 성능이 요구된다.
우리는 $\pi_\theta$를 기반으로 수행한 $a_t$가 실제 전문가가 수행한 action($\pi^{\star}(s_t)$)와 동일한 것이 이상적이므로 이때의 cost($c$)를 0 다른 경우를 1이라고 한다면 결국 우리의 목표는 $$ \underset{\theta}{max}E_{s_t \sim p_{\pi_\theta}(s_t)}\left [ c(s_t, a_t) \right] $$ 라고 할 수 있다.

이 관점에서 다시 생각하면, 만약에 $\pi_\theta$가 $\pi^{\star}$를 따르지 않을 확률이 $\epsilon$(매우 작은 값) 이하라고 할 때, trajectory 의 길이가 $T$이므로 cost의 기댓값은 $\epsilon T + (1-\epsilon)C(T-1)$이라 할 수 있다. 그리고 이 수식을 전개 해 보면 결국 시간 복잡도가 $O(T^2)$이고, $\epsilon$은 매우 작은 값이므로 Trajectory의 길이 제곱에 비례하게 된다.
그렇기 때문에 trajectory를 보면 $\pi_\theta$기반으로 action 시 초기의 작은 실수가 큰 에러로 유도됨을 이해할 수 있다.

Address problem
Be smart about how we collect and augment our data
앞서 살펴본 예제를 이어가면, 완벽한 Train data가 있다고 하더라도, 작은 mistake가 발견되면 이는 Train 과정에서 보지 못한 새로운 observation(state)이기 때문에 Trajectory가 길어짐에 따라 큰 Error를 유발하게 된다. 그렇다면 이를 해결할 수 있는 방법은 뭐가 있을까?
먼저 mistakes와 correction을 의도적으로 추가하는 방법이 있다. 이는 매 Time step 마다 $\pi^\star$처럼 행동하지는 않지만, $\pi_\theta$에서 가능한 mistakes를 고려해서 error correction이 가능하도록 할 수 있다.
또한, Data augmentation을 수행하는 것이다. 앞서 살펴본 Fake observation도 이 일종인데, 만약 mistake(data augmentation)이 랜덤하게 발생되면 이는 결국 상쇄되므로, Optimal action은 여전히 most probable 하다. 따라서 Data augmentation에 의한 random noise는 최적의 행동에 영향을 주진 않지만, 다양한 observation(state)를 가능하게 한다.

Use very powerful models that make very few mistakes
우리가 전문가의 행동을 완벽하게 따라할 수 없는 이유 중 하나는 Non-Markovian behavior이기 때문이다. 환경이 Markov 하다는 의미는 현재의 상태 $s_t$만이 미래의 상태와 보상을 예측하는데 필요한 모든 정보를 제공한다는 의미이다. 만약 Markov 하면, 동일한 state에 대해서는 동일한 action을 반복해야 한다. 하지만, 우리는 과거 동일 상태에서의 행동을 바탕으로 똫같은 상태를 마주하면 다른 행동을 한다. 즉, 이전의 관측값이 영향을 주게 된다.

그렇다면, Policy가 과거 Observations를 고려해서 의사결정을 하도록 하려면 어떻게 해야할까? 아래와 같이 모든 장면 frames를 입력으로 넣어주면 되지만, weights 가 많아지는 단점이 있다.

그래서 최근에는 Transformer 등의 sequence model을 활용해서 연속적인 observations를 처리하는 연구가 진행되고 있다. 하지만 항상 과거의 모든 정보를 입력으로 넣는게 좋을까?

우리는 모델이 본질적인 상관관계에 의존하지 않고, 비본질적 상관관계에 의존하는 Causal Confusion을 고려해야 한다.
예를 들어, Secenario A는 모든 Observations를 전부 제공하는 상황이다. 앞에 사람이 있어서 우리는 브레이크를 밟고, 브레이크가 밟히면 브레이크 등이 들어온다. 이때, 이러한 Full observations 중 중간 순열 부터는 브레이크 등이 켜졌으니 브레이크를 밟는다고 생각할 수 있게 된다.
하지만, Scenario B는 이미지의 하단 부분은 가려진 상태이다. 이제서야 전방에 사람이 있으니 브레이크를 밟는다는 본질적 상관관계를 모델이 집중할 수 있게 된다.

또다른 이유 중 하나는 Multimodal behavior이 가능하기 때문이다. 전방에 객체가 있는 동일한 state에 대해서 여러개의 action이 가능하다. 만약 우리는 왼쪽, 오른쪽, 직진이라는 3개의 action이 가능하다고 하면, policy는 왼쪽, 오른쪽 action의 확률이 높을 것이다. 이때, 단순히 평균을 내면 직진이 가장 확률이 높아지고 결국 적절한 action을 취하지 못하게 된다.

이를 해결하기 위한 첫번째 방법은 Expressive continuous distributions를 활용하는 것이다. 이는 하나의 상태에서 여러 개의 서로 다른 행동 모드를 동시에 표현할 수 있는, 표현력이 높은 연속 확률 분포 정책을 의미한다.
다양한 방법 중 첫번째는 mixture of Gaussians이다. 이는 서로 다른 Action을 서로 다른 Gaussian으로 표현하는 방법이다. 기존에는 최적의 Action을 직접 예측하였지만, 이 경우 CNN 구조를 통해 ACtion 분포를 구성하는 Gaussian parameter를 출력하게 된다. 따라서 Multimodal behaviors를 직접적으로 표현할 수 있다.

또 다른 방법은 Latent variable models를 이용하는 것이다. 이는 잠재변수(latent)를 이용해서 같은 관측에서도 서로 다른 행동 모드를 자연스럽게 생성하는 방법이다. 여러 행동들에 대해서 내가 유도하고자 하는 action이 유도되기 위해 잠재변수를 활용하는 방법이다.
아래 예시에서는, 같은 도로 환경에서도 서로 다른 $z$에 의해 서로 다른 행동 벡터가 출력되는 것을 확인할 수 있다.
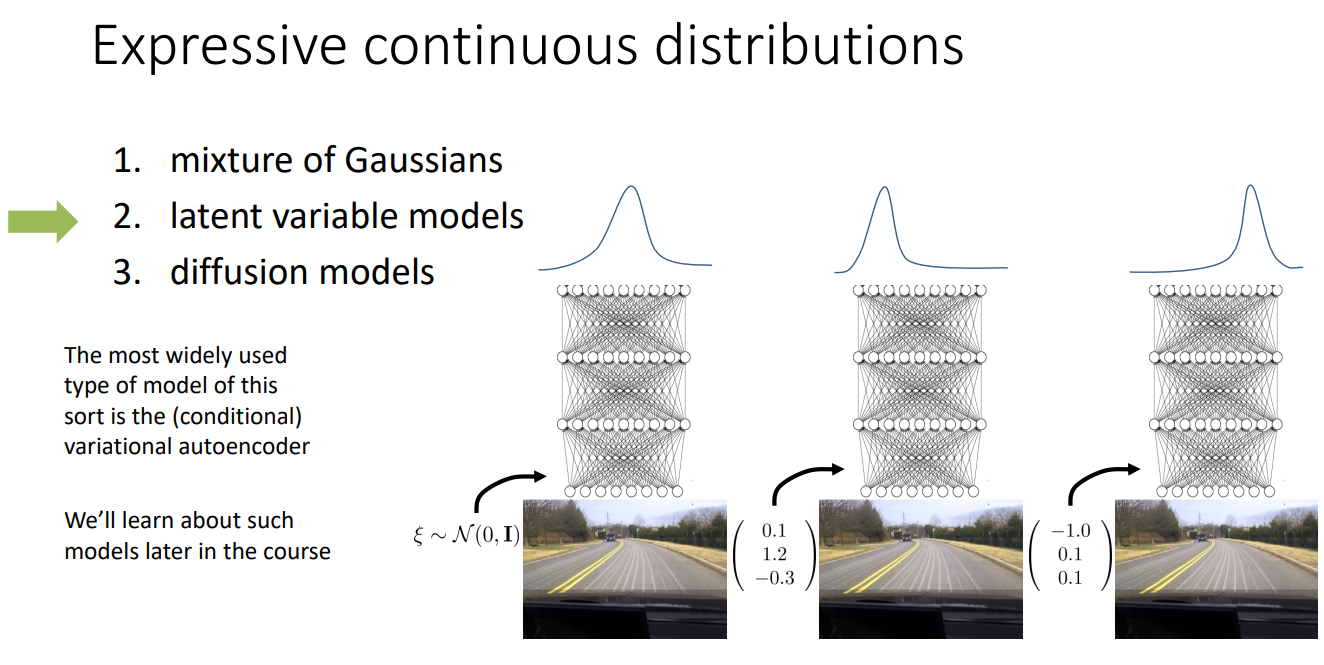
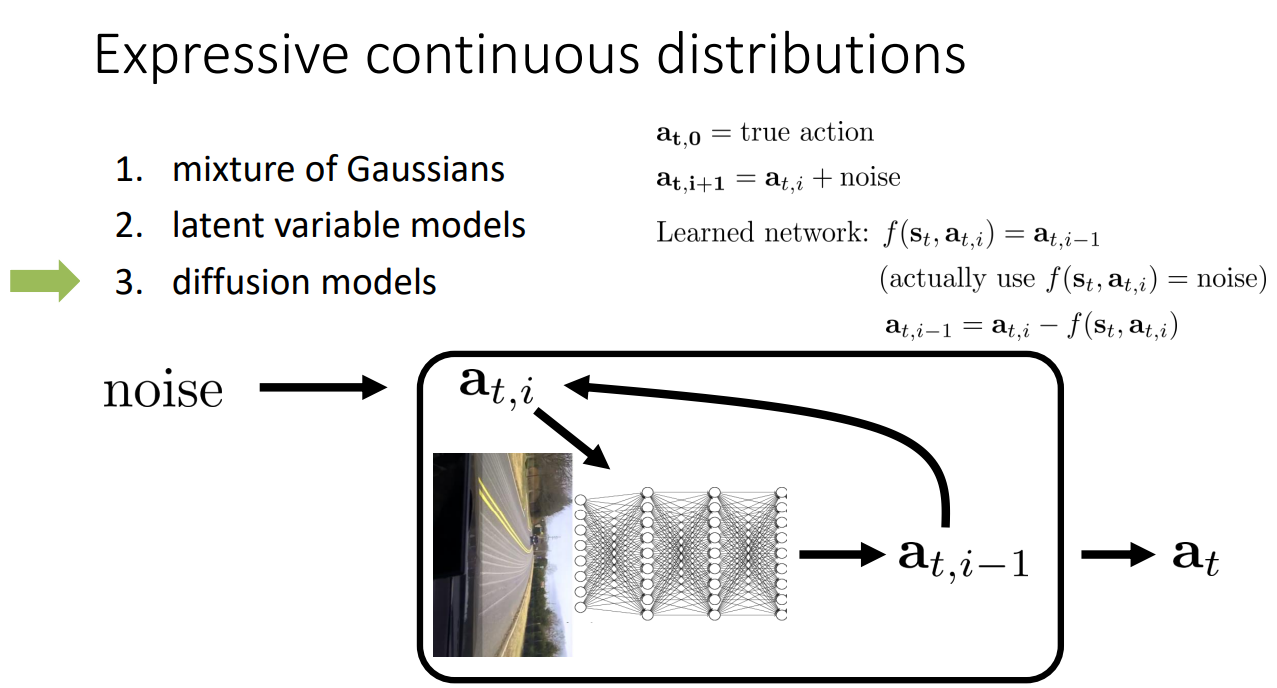
마지막으로, Diffusion models를 활용하는 방법이 있다. Diffusion model은 이미지 생성 분야에서 많이 활용되는 모델인데, 아래쪽 예시와 같이 noise를 인위적으로 추가하여 Noise를 제거하도록 학습하는 방법이다. 즉, gaussian noise를 매 step 마다 조금씩 추가하는 과정을 반복하면 $x_T /sim N(0,1)$ 즉, 아무 정보 없는 순수 노이즈가 된다. 이때, 모델은 원본을 직접 복원하는 것이 아닌, 현재 단계에 섞인 노이즈를 예측하여, 해당 노이즈를 제거한 sample을 생성하면서 학습하게 된다.

이러한 메커니즘을 활용해서 $s_t$와 noise가 추가된 $a_{t,i}$에 대해서 네트워크는 현재 단계의 noise를 출력하고, 해당 노이즈를 제거함으로써 더 최적의 action을 반환할 수 있도록 학습하는 것이 diffusion mecanism을 활용한 방법이다.
Multimodal behavior를 해결하는 다음방법은 이산화(Discretization)가 있다. 즉, 연속된 행동을 이산화하는 것이다. 예를 들어, Steering을 {-1, -0.5, 0, 0.5,1}과 같은 bin으로 나누어 생각하는 것이다. 이는 분류 문제처럼 다룰 수 있어 안정적이지만, 만약 Action vector가 고차원이라면 문제가 된다. 만약, 각 행동 차원이 $d$이고, 각 차원마다 $K$개의 bin이 있다면, 총 action의 수는 $K^d$로 기하급수적으로 늘어난다.

이러한 고차원 문제를 해결하기 위한 방법이 Autoregressive discretization이다. 즉, $d$개의 행동에 대해서 순차적으로 이산화 하는 방법이다. 아래 예시와 같이, $s_t$가 입력으로 들어오면 첫번째 action에 대해서 $K$개의 bin에 대한 예측을 진행하고, 그 결과는 $s_t$와 함께 두번째 action에 대한 예측의 입력으로 들어오게 된다. 그리고 결국 chain rule에 의해서 모든 action에 대해서 예측할 수 있게 되고, 고차원 action에 대해서도 적용할 수 있게 된다.

다양한 예시 중 RT-1은 특히 중요한 연구이니 나중에 논문으로 살펴보자

'Reinforcement Learning' 카테고리의 다른 글
| [RL] CS285: Lecture 04. Introduction to Reinforcement Learning(1) (0) | 2026.01.27 |
|---|---|
| [RL] CS285: Lecture 02. Supervised Learning of Behaviors(2) (0) | 2025.12.14 |
| [RL] CS285: Lecture 01. Introduction (0) | 2025.12.08 |
| Deep Reinforcement Learning (1) | 2024.02.05 |
| Value Function Approximation (0) | 2024.02.04 |




