| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- GIT
- CNN
- dfs
- dynamic programming
- 딥러닝
- r-cnn
- DP
- 백준
- hm3dsem
- UC Berkeley
- ubuntu
- LSTM
- opencv
- deep learning
- BFS
- CS285
- NLP
- machine learning
- MySQL
- hm3d
- 그래프 이론
- RL
- 머신러닝
- YoLO
- 강화학습
- image processing
- AlexNet
- C++
- Reinforcement Learning
- Python
- Today
- Total
JINWOOJUNG
[ 핸즈온 머신러닝 ] 2. 머신러닝 프로젝트 처음부터 끝까지...2(Data 전처리 1) 본문
본 포스팅은 Hands-On Machine Learning with Scikit-Learn, Keras & TensorFlow 2판을 토대로
공부한 내용을 정리하기 위한 포스팅입니다.
해당 도서에 나오는 Source Code 및 자료는 GitHub를 참조하여 진행하였습니다.
https://github.com/ageron/handson-ml2
GitHub - ageron/handson-ml2: A series of Jupyter notebooks that walk you through the fundamentals of Machine Learning and Deep L
A series of Jupyter notebooks that walk you through the fundamentals of Machine Learning and Deep Learning in Python using Scikit-Learn, Keras and TensorFlow 2. - ageron/handson-ml2
github.com
https://jinwoo-jung.tistory.com/94
[ 핸즈온 머신러닝 ] 2. 머신러닝 프로젝트 처음부터 끝까지...1
본 포스팅은 Hands-On Machine Learning with Scikit-Learn, Keras & TensorFlow 2판을 토대로공부한 내용을 정리하기 위한 포스팅입니다. 해당 도서에 나오는 Source Code 및 자료는 GitHub를 참조하여 진행하였습니
jinwoo-jung.com
Data Visualization
Train Set를 더 자세히 살펴보자. 위, 경도 값이 특성으로 포함되어 있기 때문에, 이를 기준으로 데이터를 시각화 할 수 있다. 이때, alpha 옵션을 통하여 밀집된 영역을 더 잘 표현할 수 있다.
from Function import *
st_DataFramePD = LoadData()
st_DataFramePD_WithID = st_DataFramePD.reset_index()
st_DataFramePD["income_cat"] = pd.cut(st_DataFramePD["median_income"],
bins=[0., 1.5, 3.0, 4.5, 6., np.inf],
labels=[1, 2, 3, 4, 5])
split = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42)
for train_index, test_index in split.split(st_DataFramePD, st_DataFramePD["income_cat"]):
st_TrainSet = st_DataFramePD.loc[train_index]
st_TestSet = st_DataFramePD.loc[test_index]
for set_ in (st_TrainSet, st_TestSet):
set_.drop("income_cat", axis=1, inplace=True)
st_TrainSetTmp = st_TrainSet.copy()
st_TrainSetTmp.plot(kind="scatter", x="longitude", y="latitude")
st_TrainSetTmp.plot(kind="scatter", x="longitude", y="latitude", alpha=0.1)
plt.show()

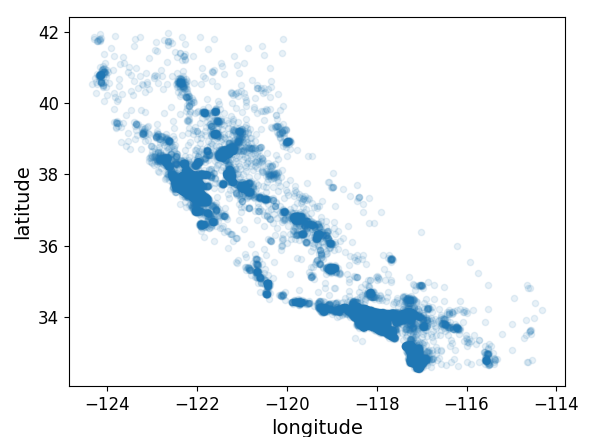
alpha 옵션을 사용한 오른쪽 결과가 밀집된 지역의 경향성을 확인하기 더 용이하다.
이젠 주택 가격을 시각화 해 보자.
- 원의 반지름 : 각 구역의 인구수
- 색상 : 가격 - 낮은 가격이 파란색, 높은 가격이 빨간색인 jet Color Map 사용
st_TrainSetTmp.plot(kind="scatter", x="longitude", y="latitude", alpha=0.4,
s=st_TrainSetTmp["population"]/100, label="population", figsize=(10,7),
c="median_house_value", cmap=plt.get_cmap("jet"), colorbar=True,
sharex=False)
이전에 시각화 한 인구 밀도가 높은 지역이 더 높은 주택 가격을 나타냄을 확인할 수 있다. 또한, 각 지역의 인구 수(원의 반지름)이 클수록 더 높은 주택 가격을 나타낸다.
상관관계
이처럼 직관적으로 주택 가격은 인구밀도와 인구 수에 비례한다고 분석할 수 있는데, 이처럼 각 특성관의 상관관계를 나타낸 것을 표준 상관계수라 한다. 이는 corr() Method를 통해 쉽게 구할 수 있다.
st_TrainSetTmp = st_TrainSetTmp.drop(columns=['ocean_proximity'])
st_CorrelationMatrix = st_TrainSetTmp.corr()
print(st_CorrelationMatrix["median_house_value"].sort_values(ascending= False))
현재 ocean_proximity 특성은 String 형태이므로 제외시킨 후 상관관계를 계산하였다.

상관관계는 -1~1의 범위를 가지며, 1에 가까우면 양의 상관관계를 가지고, -1에 가까우면 음의 상관관계를 가진다. 0에 가까울수록 선형적인 상관관계가 없음을 의미한다.
숫자형 특성 사이의 산점도를 그려줌으로써 상관관계를 확인할 수 있는데, Pandas의 scatter_matrix() Method를 활용하면 된다. median house value와 높은 상관관계를 보이는 몇몇 특성만 살펴보자.
st_TrainSetTmp = st_TrainSetTmp.drop(columns=['ocean_proximity'])
st_CorrelationMatrix = st_TrainSetTmp.corr()
attributes = ["median_house_value", "median_income", "total_rooms",
"housing_median_age"]
scatter_matrix(st_TrainSetTmp[attributes], figsize=(12, 8))
plt.show()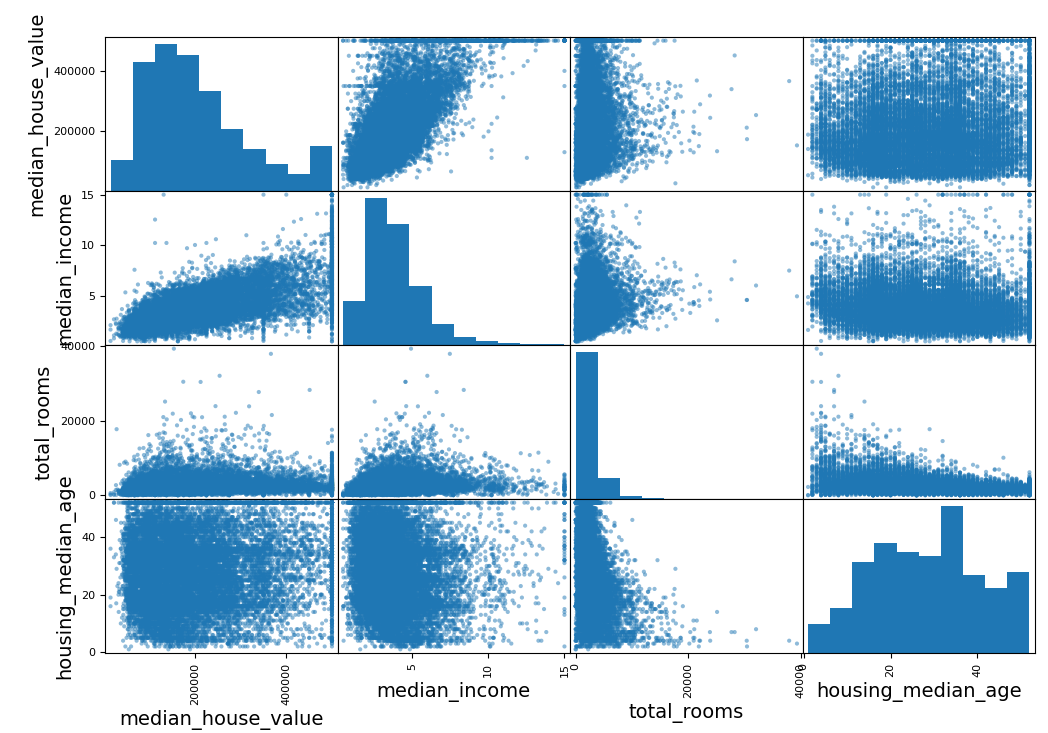
median_house_value와 가장 큰 상관관계를 보였던 median_income의 산점도 그래프를 보면 선형적인 우상향 그래프를 나타냄을 확인할 수 있다. 조금 더 자세히 살펴보자.
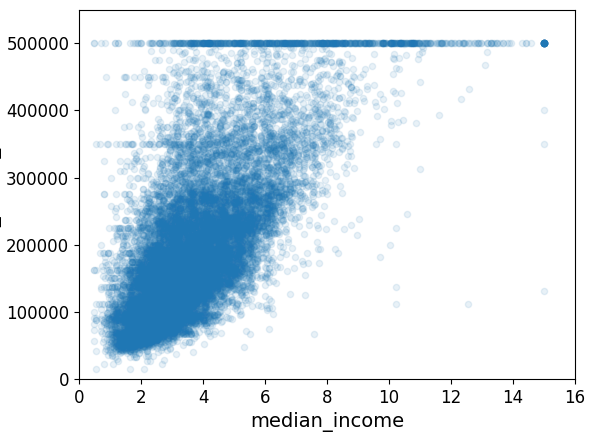
강한 우상향 그래프를 나타내지만, 500,000에서 수평선이 나타나는데, 이는 가격에 Limit가 걸려 있음을 확인할 수 있다. 또한, 350,000과 450,000 부근에도 수평선이 존재하는데, 이런 데이터는 우상향의 상관관계를 보임에 있어서 좋지 않은 데이터이므로 후처리가 요구된다.
주어진 특성들의 조합을 한번 생각 해 보자. 예시로 특정 구역의 방 개수는 얼마나 많은 가구 수가 있는지 모른다면 유용한 정보가 아니다. 즉, 우리가 진짜로 원하는 정보는 가구당 방 개수이다. 이처럼 특성들의 조합으로 새로운 특성을 만들어본다면 유용한 특성을 구할 수 있을 것이다.
st_TrainSetTmp = st_TrainSetTmp.drop(columns=['ocean_proximity'])
st_TrainSetTmp["rooms_per_household"] = st_TrainSetTmp["total_rooms"]/st_TrainSetTmp["households"]
st_TrainSetTmp["bedrooms_per_room"] = st_TrainSetTmp["total_bedrooms"]/st_TrainSetTmp["total_rooms"]
st_TrainSetTmp["population_per_household"]=st_TrainSetTmp["population"]/st_TrainSetTmp["households"]
st_CorrelationMatrix = st_TrainSetTmp.corr()
print(st_CorrelationMatrix["median_house_value"].sort_values(ascending=False))


왼쪽이 특성들의 조합으로 만든 특성들의 상관계수를 포함한 상관관계 정보이다. rooms per household 특성은 total rooms보다 median house value와의 상관관계가 더 크다는 것을 확인할 수 있다.
Data 준비
Train Set를 다시 원래 상태로 되돌린 후 예측 변수와 타깃 값에 같은 변형을 적용하지 않기 위해 예측 변수와 레이블을 drop() Method를 통해 분리시킨다.
from Function import *
st_DataFramePD = LoadData()
st_DataFramePD_WithID = st_DataFramePD.reset_index()
st_DataFramePD["income_cat"] = pd.cut(st_DataFramePD["median_income"],
bins=[0., 1.5, 3.0, 4.5, 6., np.inf],
labels=[1, 2, 3, 4, 5])
split = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42)
for train_index, test_index in split.split(st_DataFramePD, st_DataFramePD["income_cat"]):
st_TrainSetTmp = st_DataFramePD.loc[train_index]
st_TestSetTmp = st_DataFramePD.loc[test_index]
for set_ in (st_TrainSetTmp, st_TestSetTmp):
set_.drop("income_cat", axis=1, inplace=True)
st_TrainSet = st_TrainSetTmp.copy()
print(st_TrainSet.head())
print("--------------------")
st_TrainSetLable = st_TrainSet["median_house_value"].copy()
st_TrainSet = st_TrainSet.drop("median_house_value", axis=1)
print(st_TrainSet.head())
print("--------------------")
print(st_TrainSetLable.head())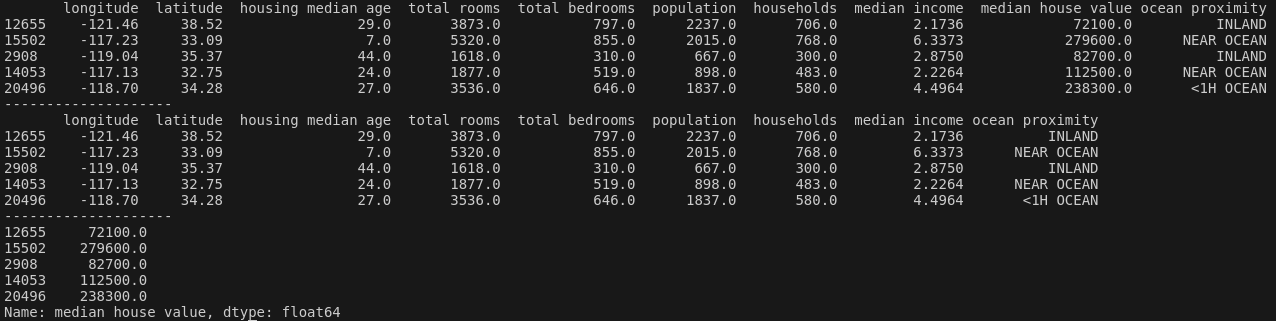
Data 전처리 - Null Value(수치형 특성)
가장 먼저 전처리 해야 할 것은 total_bedrooms 특성에 존재하는 Null Value에 대한 처리이다.
- Null Value가 있는 구역(샘플) 삭제
- Null Value가 있는 특성 삭제
- Null Value를 평균, 중간값 등으로 채움
각각에 대한 처리는 Pandas Dataframe의 dropna(), drop(), fillna() Method를 통해 처리 가능하다.
# Null Value가 존재하는 샘플 삭제
st_TrainSet.dropna(subset=["total_bedrooms"])
# Null Value가 존재하는 특성 삭제
st_TrainSet.drop("total_bedrooms", axis=1)
# Null Value를 평균값으로 채움
f32_MedianValue = st_TrainSet["total_bedrooms"].median()
st_TrainSet["total_bedrooms"].fillna(f32_MedianValue, inplace = True)
sklearn의 SimpleImputer는 Null Value를 손쉽게 처리하게 해 준다.
from sklearn.impute import SimpleImputer
st_Imputer = SimpleImputer(strategy="median") # SimpleImputer 객체 생성
st_TrainSetNum = st_TrainSet.drop("ocean_proximity", axis = 1) # Text 특성 제외
st_Imputer.fit(st_TrainSetNum) # 각 특성의 Median Value 계산
st_Result = st_Imputer.transform(st_TrainSetNum) # Null Value -> Median Value 적용
# Pandas Dataframe으로 변환
st_TrainSetNum = pd.DataFrame(st_TrainSetNum, columns=st_TrainSetNum.columns,
index=st_TrainSetNum.index)
위와 같은 흐름으로 각 특성에 대하여 평균값을 계산한 뒤 누락된 값을 평균값으로 대체할 수 있다.
실제로 SimpleImputer 객체가 계산한 각 특성의 평균값과 Pandas Dataframe에서 계산한 평균값을 비교 해 보면 동일함을 확인할 수 있다.
print(st_Imputer.statistics_)
print("---------------")
print(st_TrainSetNum.median().values)
describe() Method를 통해 각 특성의 데이터를 살펴보면

total bedrooms의 개수가 Null Value 없이 채워졌음을 확인할 수 있다.
Data 전처리 - 텍스트/범주형 특성
이제부터 수치형이 아닌 텍스트 특성을 살펴보자.
st_TrainSetString = st_TrainSet[["ocean_proximity"]]
print(st_TrainSetString.head(10))
ocean_proximity 특성이 텍스트이므로 살펴보면 다음과 같다.
ocean proximity 즉, 해안 근접도 특성은 단순한 텍스트 특성이 아니라, 각 구역의 위치에 따른 범주형 특성이다. unique() Method를 사용해서 각 범주를 살펴보면 다음과 같다.
print(st_TrainSetString["ocean_proximity"].unique())

따라서 범주형 특성을 텍스트에서 숫자로 변환하자. 이 과정에서 sklearn의 OrdinalEncoder Class를 사용한다.
from sklearn.preprocessing import OrdinalEncoder
st_OrdinalEncoder = OrdinalEncoder()
st_TrainSetString_Encoded = st_OrdinalEncoder.fit_transform(st_TrainSetString)
print(st_TrainSetString_Encoded[:10])


앞서 살펴본 ocean proximity 특성의 상위 10개의 샘플에 대한 변환 결과를 확인해보자. 각 범주형 특성의 카테고리 ID에 맞게 숫자형으로 변환됨을 확인할 수 있다.
이처럼 범주형 특성의 카테고리들을 살펴보고 싶으면 categories_ 인스턴스 변수로 확인할 수 있다.
print(st_OrdinalEncoder.categories_st_OrdinalEncoder)
하지만, 위와같은 단순한 변환은 학습 과정에서 오해를 일으킬 수 있다. 일반적으로 머신러닝 알고리즘은 가까운 두 값이 떨어져 있는 두 값보다 더 비슷하다고 생각하기 때문이다. 단순히 좋고 나쁨으로 표현된 텍스트형 특성이었다면 상관없지만, ocean proximity와 같은 특성에 있어서 변환되는 두 숫자는 각 카테고리와 상관이 없기 때문이다.
따라서 이런경우 One-Hot Encoding으로 해결 가능하다. One-Hot Encoding은 해당되는 카테고리만 1이고 나머진 모두 0으로 Encoding하게 된다. sklearn은 OneHotEncoder Class를 제공한다.
from sklearn.preprocessing import OneHotEncoder
st_OneHotEncoder = OneHotEncoder()
st_TrainSetString_Encoded = st_OneHotEncoder.fit_transform(st_TrainSetString)
print(st_TrainSetString_Encoded.toarray())
One-Hot Encoding 결과는 희소 행렬(Sparse Matrix)이다. 당연히 각 구역별로 해당되는 카테고리만 1이고 나머지는 0이기 때문이다. 따라서 이러한 Encoding 방식은 방대한 카테고리를 가지고 있는 범주형 특성을 다루기에 매우 효율적인데, 이는 단순히 1인 위치만 저장하면 되기 때문이다.


앞서 OrdinalEncoder를 이용해 변환한 결과와 동일하게 각 카테고리에 맞게 잘 Encoding 됨을 확인할 수 있다.
나만의 변환기
sklearn에서 제공하는 것 외에 자신만의 변환기가 필요하다. 또한, 이를 sklearn에서 제공하는 Method()와 같이 연동하고 싶다면, fit(), transform() 등의 Method를 갖게 구현하면 된다. 이를 위해서는 BaseEstimator, TransformerMixin Class를 상속하면 된다.
BaseEstimator Class를 상속함으로써 HyperParameter 튜닝에 필요한 get_params(), set_params() 등의 Method()를 사용할 수 있으며, TransformerMixin Class를 상속함으로써 fit_transform() Method를 구현없이 자동으로 사용할 수 있다.
from sklearn.base import BaseEstimator, TransformerMixin
s32_RoomIdx, s32_BedRoomsIdx, s32_PopulationIdx, s32_HouseholdsIdx = 3, 4, 5, 6 # Dataframe에서 각 특성에 해당되는 열번호
class CombinedAttributesAdder(BaseEstimator, TransformerMixin):
def __init__(self, add_bedrooms_per_room=True):
self.add_bedrooms_per_room = add_bedrooms_per_room
def fit(self, X, y=None):
return self # 아무것도 하지 않음
def transform(self, X):
rooms_per_household = X[:, s32_RoomIdx] / X[:, s32_HouseholdsIdx] # 각 샘플에 대하여 가정수를 방 수로 나눔으로써 가정당 방 개수 특성을 새롭게 계산함
population_per_household = X[:, s32_PopulationIdx] / X[:, s32_HouseholdsIdx] # 각 샘플에 대하여 가정수를 인구 수로 나눔으로써 가정당 인구 개수 특성을 새롭게 계산함
if self.add_bedrooms_per_room:
bedrooms_per_room = X[:, s32_BedRoomsIdx] / X[:, s32_RoomIdx] # 각 샘플에 대하여 방 수를 침실 수로 나눔으로써 방당 침실 수 특성을 새롭게 계산함
return np.c_[X, rooms_per_household, population_per_household, # np.c_()를 통해 입력받은 numpy 배열(Dataframe의 값들)에 계산한 특성들을 새롭게 추가함
bedrooms_per_room]
else:
return np.c_[X, rooms_per_household, population_per_household]
코드적으로 어려운 부분은 없어서 주석으로 대체하겠다.
print(st_TrainSet.head())
st_Transformer = CombinedAttributesAdder(add_bedrooms_per_room=False) # 연습 용도로 방당 침실수를 추가하지 않음
st_TrainSetAdded = st_Transformer.transform(st_TrainSet.to_numpy())
st_TrainSet = pd.DataFrame(
st_TrainSetAdded,
columns=list(st_TrainSet.columns)+["rooms_per_household", "population_per_household"],
index=st_TrainSet.index)
print(st_TrainSet.head())
원본 Train Set인 st_TrainSet의 상위 5개의 항목을 출력 해 보면 다음과 같다.

앞서 선언한 Idx 변수들이 각 특성에 해당되는 열 번호임을 확인할 수 있다. 따라서 선언한 CombinedAttributesAdder() 객체를 생성하고, add_bedrooms_per_room은 False로 하여 해당 특성은 생성하지 않도록 하였다. 생성한 객체의 transform() Method에 원본 Train Set을 Numpy 배열로 변환하여 넣어줌으로써 새로운 특성인 rooms_per_household, population_per_household가 계산되고, np.c_()를 통해 해당 특성들이 추가된 Numpy 배열이 반환된다. 이를 다시 Pandas Dataframe으로 바꿔주는데, 추가되는 열 특성의 이름을 추가 해 준다.

비교 결과 원하는 특성이 추가되어 잘 변환됨을 확인할 수 있다.
Reference
'핸즈온머신러닝' 카테고리의 다른 글
| [ 핸즈온 머신러닝 ] 3. 분류...1(Binary Classifier) (14) | 2024.08.29 |
|---|---|
| [ 핸즈온 머신러닝 ] 2. 머신러닝 프로젝트 처음부터 끝까지...3(Model 선정) (2) | 2024.08.27 |
| [ 핸즈온 머신러닝 ] 2. 머신러닝 프로젝트 처음부터 끝까지...2(Data 전처리) (0) | 2024.08.20 |
| [ 핸즈온 머신러닝 ] 2. 머신러닝 프로젝트 처음부터 끝까지...1(데이터 분석) (0) | 2024.08.18 |
| [ 핸즈온 머신러닝 ] 1-1. 한눈에 보는 머신러닝 (0) | 2024.08.17 |



