| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- Reinforcement Learning
- CS285
- dynamic programming
- machine learning
- GIT
- MySQL
- deep learning
- 그래프 이론
- r-cnn
- 머신러닝
- LSTM
- dfs
- UC Berkeley
- BFS
- hm3dsem
- NLP
- DP
- YoLO
- 강화학습
- C++
- image processing
- hm3d
- RL
- 딥러닝
- Python
- CNN
- 백준
- AlexNet
- opencv
- ubuntu
- Today
- Total
JINWOOJUNG
[ 핸즈온 머신러닝 ] 3. 분류...1(Binary Classifier) 본문
본 포스팅은 Hands-On Machine Learning with Scikit-Learn, Keras & TensorFlow 2판을 토대로
공부한 내용을 정리하기 위한 포스팅입니다.
해당 도서에 나오는 Source Code 및 자료는 GitHub를 참조하여 진행하였습니다.
https://codingalzi.github.io/handson-ml2/
핸즈온 머신러닝
머신러닝/딥러닝 기초 지식 제공
codingalzi.github.io
https://jinwoo-jung.tistory.com/97
[ 핸즈온 머신러닝 ] 2. 머신러닝 프로젝트 처음부터 끝까지...3(Model 선정)
본 포스팅은 Hands-On Machine Learning with Scikit-Learn, Keras & TensorFlow 2판을 토대로공부한 내용을 정리하기 위한 포스팅입니다. 해당 도서에 나오는 Source Code 및 자료는 GitHub를 참조하여 진행하였습니
jinwoo-jung.com
분류(Classification)을 학습하기 위해서 고등학생과 미국 인구조사국 직원들이 손으로 쓴 70,000개의 작은 숫자 이미지를 모은 MNIST 데이터셋을 사용할 것이다.
MNIST Dataset
from Function import *
from sklearn.datasets import fetch_openml
mnist = fetch_openml('mnist_784', version=1)
print(mnist.keys())
Function에서 불러오는 함수들은 내가 가지고 있는 함수들이기에 무시하자.
sklearn을 통해 데이터셋을 불러오면 유사한 Dictionary 구조를 가지게 된다.
- DESCR Key : Information of Dataset
- data Key : 샘플이 하나의 행, 특성이 하나의 열로 구성된 배열
- target Key : Label 배열

실제로, fetch_openml() Methcod를 통해 불러온 MNIST Dataset도 유사한 구조를 가지고 있다.
X, y = mnist["data"], mnist["target"]
print(X.shape)
print(y.shape)
Dictonary는 위와 같이 []안에 Key Value를 입력해서 접근할 수 있다.
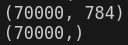
MNIST Dataset은 70,000개의 샘플과 784개의 특성이 있음을 확인할 수 있는데, 이는 각 샘플이 28x28 영상이기 때문이다(픽셀 개수 만큼 각 샘플의 특성 존재). 각각의 특성은 픽셀이기에 0~255의 Value를 가진다.
target의 경우 70,000개의 샘플의 정답값을 가지기에 70,000개임을 쉽게 유추할 수 있다.
# X, y를 NumPy 배열로 변환
X, y = mnist["data"].to_numpy(), mnist["target"].to_numpy()
# 첫 번째 샘플 선택
st_Sample = X[0]
st_SampleImage = st_Sample.reshape(28, 28)
# 첫 번째 레이블 선택 및 출력
st_SampleLable = y[0]
print("st_SampleLable: ", int(st_SampleLable)) # 레이블을 정수로 변환 후 출력
# 이미지 출력
plt.imshow(st_SampleImage, cmap="binary")
plt.axis("off")
plt.show()
이때, X는 pandas.core.frame.Datafrmae Type이고, y는 pandas.core.series.Series Type이므로 numpy Array 형태로 변환해야 한다.

첫번째 영상을 가져와 영상으로 변환하여 출력하면 다음과 같은데, 실제 Lable역시 5임을 확인할 수 있다. 하지만 Lable을 가지는 target Key의 경우 문자열이기에 숫자형으로 출력하면 역시 5임을 확인할 수 있다.
이진 분류기(Binary Classifer)
먼저 가장 간단한 이진 분류기를 훈련시켜 보자 즉, '숫자 5임','숫자 5가 아님' 이렇게 2가지로 분류하는 이진 분류기이다. 분류 모델은 확률적 경사 하강법(Stochastic Gradient Descent, SGD) 분류기로 해보자.
from Function import *
from sklearn.datasets import fetch_openml
from sklearn.linear_model import SGDClassifier
# MNIST 데이터셋 로드
mnist = fetch_openml('mnist_784', version=1)
# X, y를 NumPy 배열로 변환
X, y = mnist["data"].to_numpy(), mnist["target"].to_numpy()
y = y.astype(np.uint8) # String -> uint8
st_Sample = X[0]
# Train, TestSet 분류
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
#######################################################################
########################## Binary Classifier ##########################
#######################################################################
y_train_5 = (y_train == 5)
y_test_5 = (y_test == 5)
print(y_train)
print(y_train_5)
st_SGDClassifier = SGDClassifier(max_iter=1000, tol=1e-3, random_state=42)
st_SGDClassifier.fit(X_train, y_train_5)
print(st_SGDClassifier.predict([st_Sample]))
MNIST Dataset의 경우 앞쪽 60,000개의 이미지는 TrainSet, 나머지는 TestSet으로 분류되어 있다. 숫자 5를 구별하는 이진 분류기를 만들기 위하여 TrainSet, TestSet을 재분류 하였다.

Lable의 경우 astype()을 통해 uint8 DataType으로 변환하였으며, 그에 맞게 이진 분류기의 정답 Lable이 잘 설정됨을 확인할 수 있다.
SGD Classifier의 경우 학습 과정에서 무작위성을 사용하기에, random_state 매개변수를 지정 해 주었다. 이후 훈련시킨 모델을 기반으로 Lable이 5인 Train Sample을 입력하여 예측한 결과 다음과 같이 True임을 확인할 수 있다.
# 성능 평가 : k-겹 교차 검증
st_Score = cross_val_score(st_SGDClassifier, X_train, y_train_5, cv = 3, scoring="accuracy")
print(st_Score)
성능 평가 : k-겹 교차 검증
해당 모델의 성능 평가를 k-겹 교차 검증을 통해 평가 해 보자. 여기서는 TrainSet를 3개의 폴드로 나누고, 각 폴드에 대해 예측을 만들고 평가하기 위해 나머지 폴드로 훈련한 모델을 사용한다.

실제로 모든 폴드에 대하여 95%이상의 정확도를 보임을 확인할 수 있다. 하지만 믿을 수 있는 분류기일까?
class Never5Classifier(BaseEstimator):
def fit(self, X, y=None):
pass
def predict(self, X):
return np.zeros((len(X), 1), dtype=bool)
st_Never5Classifier = Never5Classifier()
st_TmpScore = cross_val_score(st_Never5Classifier, X_train, y_train_5, cv = 3, scoring="accuracy")
print(st_TmpScore)
무조건 False만 반환하는 분류기를 생성해서 k-겹 교차 검증을 진행한 결과 역시

90%가 넘는 정확도를 보인다. 즉, TrainSet 자체에 Lable이 5인 Data가 원래부터 적기에 높은 정확도를 보일 수 있다는 것이다.
즉, 단순한 정확도는 분류기의 성능 측정 지표로 효과적으로 동작할 수 없다!
성능 평가 : 오차 행렬(Confusion Matrix)
분류기의 성능 평가에 더 효과적인 것은 오차 행렬(Confusion Matrix)이다. 간단히 설명하자면 A Lable을 지닌 샘플이 B Lable로 분류된 횟수를 세는 것이다. 오차 행렬 계산을 위한 예측은 cross_val_predict()를 통해 구할 수 있는데, 이는 k-겹 교차 검증을 수행하는 과정에서 각 테스트 폴드에서 얻은 예측을 반환한다.
# 성능 평가 : 오차 행렬
from sklearn.model_selection import cross_val_predict
from sklearn.metrics import confusion_matrix
y_train_pred = cross_val_predict(st_SGDClassifier, X_train, y_train_5, cv=3)
st_ConfusionMatrix = confusion_matrix(y_train_5, y_train_pred)
print(st_ConfusionMatrix)
간단하게 오차행렬을 분석 해 보자. 오차 행렬의 행은 실제 클래스, 오차 행렬의 열은 예측한 클래스이다. 따라서, 1행 1열은 실제 5가 아닌 샘플을 5가 아니라고 분류한 개수(True Negative)이고, 2행 2열은 실제 5인 샘플을 5라고 분류한 개수(True Positive)이다. 1행 2열의 경우 5가 아닌 샘플을 5라고 잘못 분류한 개수(False Positive)이며, 2행 1열의 경우 5이지만 5가 아니라고 잘못 분류한 개수(True Negative)이다. 만약, 완벽한 분류기라면 대각 원소만 0이 아닌 값인 오차 행렬이 나올 것이다.
오차 행렬이 주는 값을 요약하는 지표들이 존재하는데, 먼저 정밀도(Precision)이다. 정밀도는 양성 예측의 정확도를 의미한다.
$$ 정밀도 = \frac{TP}{TP+FP}$$
정밀도는 일반적으로 재현율(Recall)과 같이 사용되는데, 재현율은 분류기가 정확하게 감지한 양성 샘플의 비율이다.
정밀도와 재현율의 관계는 다른 포스팅에서 자세히 설명했으니 참고 바란다.
https://jinwoo-jung.tistory.com/93
[ YOLOv8 ] 학습된 모델 성능 분석(Confusion Matrix, Precision, Recall, Confidence, NMS)
직접 구축한 Custom Datset을 기반으로 Yolov8 모델을 학습시켰다. 이제는 학습된 모델의 성능을 평가하기 위한 몇가지 방법을 알아보고, Yolo 모델을 학습 시 Validation Dataset을 기반으로 자동으로 계산
jinwoo-jung.com
from sklearn.metrics import precision_score, recall_score
from sklearn.metrics import f1_score
f32_PrecisionScore = precision_score(y_train_5, y_train_pred)
f32_RecallScore = recall_score(y_train_5, y_train_pred)
f32_F1Score = f1_score(y_train_5, y_train_pred)
print("PrecisionScore: ", f32_PrecisionScore, "\nRecallScore: ", f32_RecallScore, "\nF1Score: ",f32_F1Score)
각각을 계산하여 출력하면 다음과 같다.

5를 감지하는 SGD Classifier 기반 이진 분류기의 성능은 꽤 부정확하다. 5로 판별된 이미지 중 83.7%가 정확하며, 전체 숫자 5 중 65.1%만 감지했음을 확인할 수 있다.
정밀도와 재현율 두 지표를 하나로 만든것이 $F_1 Score$인데, 이는 정밀도와 재현율의 조화평균이다.
$$ F_1 = \frac{2}{\frac{1}{정밀도} + \frac{1}{재현율}} = 2 \times \frac{정밀도 \times 재현율}{정밀도 + 재현율}$$
정밀도는 0.73인데, 이 수치가 좋다고 할 수 있을까? 정밀도와 재현율이 비슷한 분류기는 $F_1$ Score가 높다. 하지만 각 모델의 기능에 다라서 정밀도 혹은 재현율이 더 중요할 수 있다. 하지만, 정밀도와 재현율 두 지표 모두를 얻을 순 없는데, 이를 정밀도/재현율 트레이드오프라고 한다.
정밀도/재현율 트레이드오프
SGD Classifier가 동작하는 원리를 알아보면서 정밀도/재현율 트레이드오프를 이해 해 보자. SGD Classifier의 경우 결정 함수(Decision Function)를 사용하여 각 샘플의 점수를 계산한 뒤, 해당 점수와 임계값(Threshold)를 이용하여 이진 분류를 진행한다.

각각의 임계값에 따라서 각 샘플이 음성/양성으로 서로 다르게 분류되고 그에 따라 정밀도와 재현율이 변화됨을 확인할 수 있다. 즉, 두가지 지표 모두를 높가 가질 순 없다.
그렇다면 어떻게 하면 적절한 Threshold를 계산할 수 있을까? cross_val_predict()의 method를 "decision_function"으로 하여 모든 샘플의 점수를 구한 뒤, precision_recall_curve()를 통해 가능한 모든 임계값에 대하여 정밀도와 재현율을 계산 해 보자.
from sklearn.metrics import precision_recall_curve
y_scores = cross_val_predict(st_SGDClassifier, X_train, y_train_5, cv=3, method="decision_function")
precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores)
# 정밀도와 재현율 그래프 그리기. x 축은 임곗값을 가리킴.
def plot_precision_recall_vs_threshold(precisions, recalls, thresholds):
plt.plot(thresholds, precisions[:-1], "b--", label="Precision", linewidth=2) # 정밀도 어레이 마지막 항목 무시
plt.plot(thresholds, recalls[:-1], "g-", label="Recall", linewidth=2) # 재현율 어레이 마지막 항목 무시
plt.legend(loc="center right", fontsize=16)
plt.xlabel("Threshold", fontsize=16)
plt.grid(True)
plt.axis([-50000, 50000, 0, 1])
# 정밀도 90%가 달성되는 지점에서의 재현율과 임곗값
recall_90_precision = recalls[np.argmax(precisions >= 0.90)]
threshold_90_precision = thresholds[np.argmax(precisions >= 0.90)]
# 빨강 점과 빨강 점선 그리기
plt.figure(figsize=(8, 4))
plot_precision_recall_vs_threshold(precisions, recalls, thresholds)
plt.plot([threshold_90_precision, threshold_90_precision], [0., 0.9], "r:") # 수직 빨강 점선
plt.plot([-50000, threshold_90_precision], [0.9, 0.9], "r:") # 위 수평 빨강 점선
plt.plot([-50000, threshold_90_precision], [recall_90_precision, recall_90_precision], "r:") # 아래 수평 빨강 점선
plt.plot([threshold_90_precision], [0.9], "ro") # 위 빨강 점
plt.plot([threshold_90_precision], [recall_90_precision], "ro") # 아래 빨강 점
save_fig("precision_recall_vs_threshold_plot")
plt.show()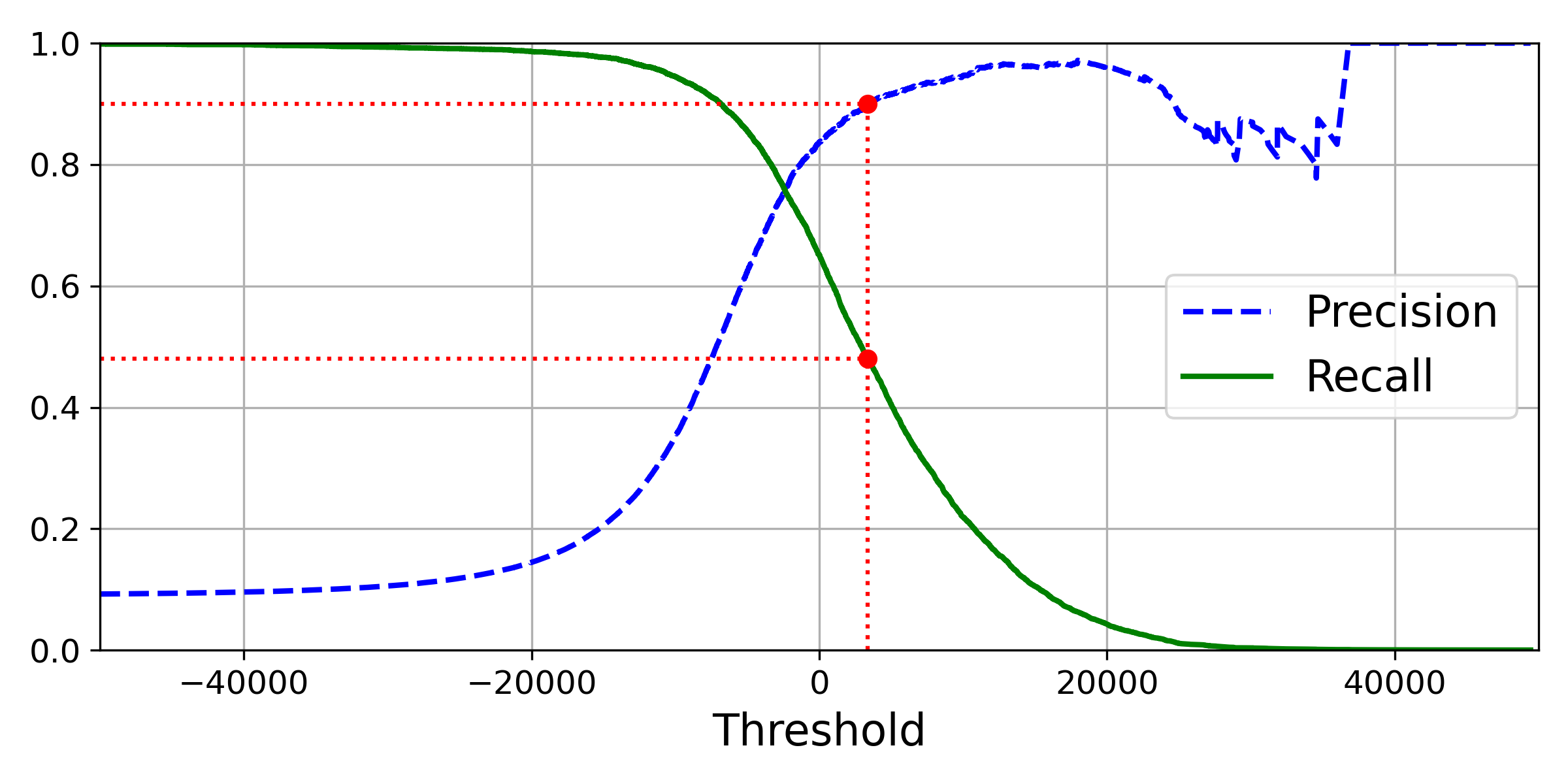
결과는 위와 같다. 여기서 빨간색은 정밀도가 90%일 때, 재현율과 임계값을 나타낸 것이다. 임계값이 커질수록, 재현율은 부드럽게 갑소하지만, 정밀도는 울퉁불퉁하는 것을 확인할 수 있는데, 이는 임계값을 올리더라도 정밀도가 일반적으론 올라가지만, 가끔 낮아질 때가 있기 때문이다.
여기서 좋은 정밀도/재현율 트레이드오프를 선택하는 다른 방법은 재현율에 대한 정밀도 곡선을 그리는 것이다.
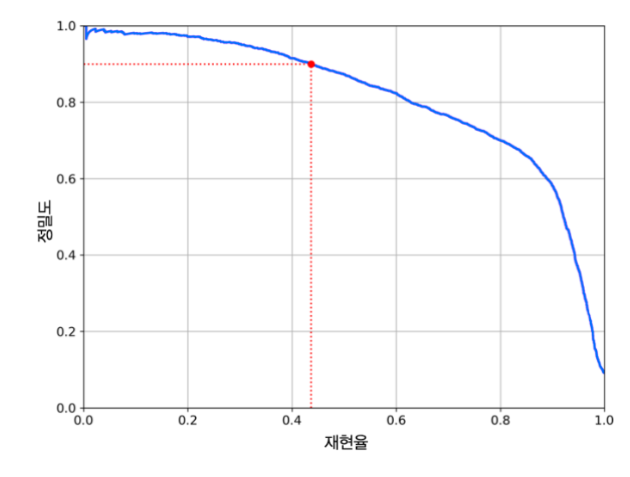
재현율이 80% 부근에서 정밀도가 급격히 하락함을 확인할 수 있는데, 이 하강점 직전을 선택하는 것이 좋다. 하지만 이것은 각 프로젝트 혹은 모델의 목적에 따라 달라진다.
하지만 정밀도가 높지만, 재현율이 너무 낮다면 좋은 모델이라고 할 수 있을까...!?
ROC 곡선
수신기 조작 특성(Receiver Operating Characteristic, ROC) 곡선을 알아보자. ROC 곡선은 거짓 양성 비율(False Positive Rate, FPR)에 대한 진짜 양성 비율(True Positive Rate, TDR = 재현율)이다. 이때, FPR은 양성으로 잘못 분류된 음성 샘플의 비율로 1에서 음성으로 정확하게 분류한 음성 샘플의 비율인 진짜 음성 비율(True Negative Rate, TNR = 특이도)을 뺀 값이다.
$$ FPR = \frac{FP}{FP+TN} = 1 - \frac{TN}{FP+TN} = 1 - TNR$$
ROC 곡선을 그리기 위해선 roc_curve() 함수를 통해 여러 임곗값에서의 TPR, FPR을 계산해야 한다.
from sklearn.metrics import roc_curve
fpr, tpr, thresholds = roc_curve(y_train_5, y_scores)
# SGD 분류기 모델의 TPR과 FPR 사이의 관계 그래프 그리기
def plot_roc_curve(fpr, tpr, label=None):
plt.plot(fpr, tpr, linewidth=2, label=label)
plt.plot([0, 1], [0, 1], 'k--') # 대각 점선
plt.axis([0, 1, 0, 1])
plt.xlabel('False Positive Rate (Fall-Out)', fontsize=16)
plt.ylabel('True Positive Rate (Recall)', fontsize=16)
plt.grid(True)
plt.figure(figsize=(8, 6))
plot_roc_curve(fpr, tpr)
# 정밀도가 90%를 넘어설 때의 재현율(TPR, 참 양성 비율)에 해당하는 거짓 양성 비율(FPR)
fpr_90 = fpr[np.argmax(tpr >= recall_90_precision)] # 0.0053 정도
# 빨강 점과 원점 사이의 실선 그리기
plt.plot([fpr_90, fpr_90], [0., recall_90_precision], "r:") # 수직 빨강 점선. 좌표는 (0.0053, 0.48) 정도
plt.plot([0.0, fpr_90], [recall_90_precision, recall_90_precision], "r:") # y축과 빨강 점 사이의 수평 빨강 점선(거의 안보임))
plt.plot([fpr_90], [recall_90_precision], "ro") # 빨강 점
save_fig("roc_curve_plot")
plt.show()
이때, recall_90_precision은 계속해서 살펴본 정밀도가 90%가 될 때 이다. 그때의 재현율은 43.68%임을 기억하고 결과를 확인 해 보자.

여기에서도 트레이드오프가 발생하는데, 재현율(TPR)이 높아질수록, 거짓 양성(FPR)이 증가함을 확인할 수 있다. 점선으로 표시되는 것은 완전한 랜덤 분류기의 ROC 곡선으로, 좋은 분류기는 점선에서 최대한 멀리(왼쪽 위 모서리) 떨어져야 한다.
곡선 아래의 면적(Area Under the Curve, AUC)를 측정하면 분류기들을 비교할 수 있다. 만약 완벽한 분류기라면, ROC의 AUC가 1, 완전 랜덤한 분류기는 AUC가 0.5가 된다.
from sklearn.metrics import roc_auc_score
print(roc_auc_score(y_train_5, y_scores))
그렇다면, RandomForestClassifier를 훈련시켜, SGDClassifier과 성능을 비교해 보자.
RandomForestClassifier는 decision_function() 대신 predict_proba() Method가 존재한다. 이는 샘플이 행, 클래스가 열이고 샘플이 주어진 클래스에 속할 확률을 담은 배열을 반환한다.
from sklearn.ensemble import RandomForestClassifier
st_RandomForestClassifier = RandomForestClassifier(random_state=42)
y_probas_forest = cross_val_predict(st_RandomForestClassifier, X_train, y_train_5, cv=3, method="predict_proba")
print(y_probas_forest)
y_train_5는 5이면 True, 아니면 False이므로 각각의 샘플이 True, False일 확률이 y_probas_forest에 저장된다.
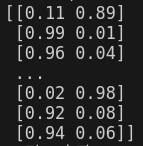
앞서 사용 한 것처럼, roc_curve()는 파라미터로 레이블과 점수를 기대하기에, 점수 대신 확률을 입력값으로 해서 ROC 곡선을 그려보자.
y_scores_forest = y_probas_forest[:, 1] # 점수 = 양성 클래스의 확률
fpr_forest, tpr_forest, thresholds_forest = roc_curve(y_train_5,y_scores_forest)
# 램덤 포레스트 분류기의 ROC 곡선 그리기
recall_for_forest = tpr_forest[np.argmax(fpr_forest >= fpr_90)] # 90% FPR에 대응하는 TPR. 약 0.95
plt.figure(figsize=(8, 6))
# 파랑 점 곡선: SGD 분류기의 ROC 곡선
plt.plot(fpr, tpr, "b:", linewidth=2, label="SGD")
# 파랑 실선: 랜덤 포레스트 분류기의 ROC 곡선
plot_roc_curve(fpr_forest, tpr_forest, "Random Forest")
plt.plot([fpr_90, fpr_90], [0., recall_90_precision], "r:") # 짧은 빵강 수직 점선
plt.plot([0.0, fpr_90], [recall_90_precision, recall_90_precision], "r:") # 아랫쪽 빨강 수평 점선 (거의 안보임)
plt.plot([fpr_90], [recall_90_precision], "ro") # 아래쪽 빨강 점. 좌표는 (0.0053, 0.48) 정도
plt.plot([fpr_90, fpr_90], [0., recall_for_forest], "r:") # 윗쪽 빨강 수평 점선 (거의 안보임)
plt.plot([fpr_90], [recall_for_forest], "ro") # 위쪽 빨강 점. 좌표는 (0.0053, 0.95) 정도
plt.grid(True)
plt.legend(loc="lower right", fontsize=16)
save_fig("roc_curve_comparison_plot")
plt.show()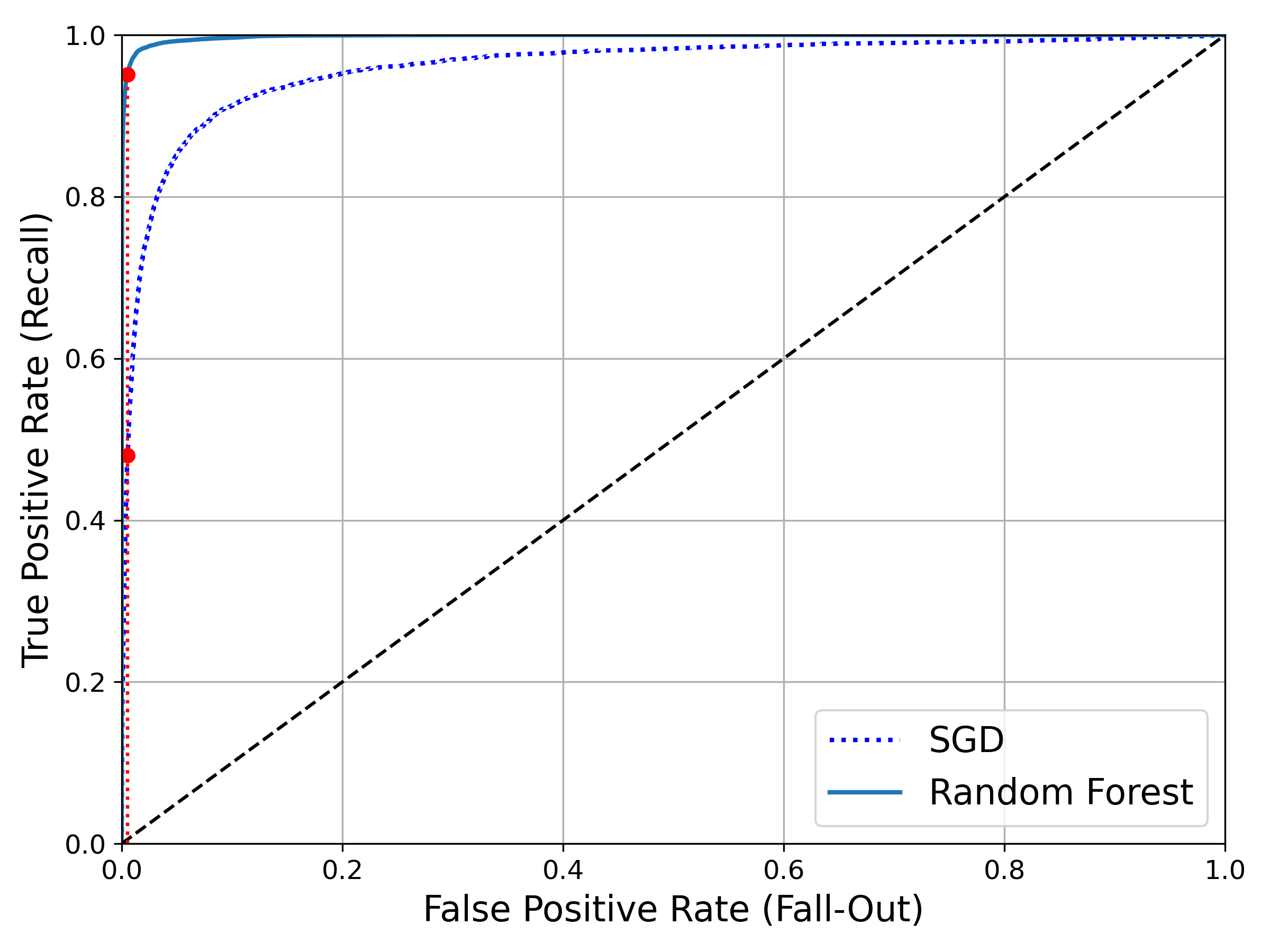
RandomForest Classifier의 ROC 곡선이 왼쪽 위 모서리에 더 가깝기에 SGD Classifier보다 성능이 더 좋음을 알 수 있으며, 당연하게 AUC도 더 큼을 알 수 있다.
'핸즈온머신러닝' 카테고리의 다른 글
| [ 핸즈온 머신러닝 ] 3. 분류...2(MultiClass Classifier) (2) | 2024.09.05 |
|---|---|
| [ 핸즈온 머신러닝 ] 2. 머신러닝 프로젝트 처음부터 끝까지...3(Model 선정) (2) | 2024.08.27 |
| [ 핸즈온 머신러닝 ] 2. 머신러닝 프로젝트 처음부터 끝까지...2(Data 전처리) (0) | 2024.08.20 |
| [ 핸즈온 머신러닝 ] 2. 머신러닝 프로젝트 처음부터 끝까지...2(Data 전처리 1) (0) | 2024.08.20 |
| [ 핸즈온 머신러닝 ] 2. 머신러닝 프로젝트 처음부터 끝까지...1(데이터 분석) (0) | 2024.08.18 |




