| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- AlexNet
- image processing
- 그래프 이론
- 백준
- hm3d
- opencv
- DP
- GIT
- RL
- NLP
- ubuntu
- dfs
- C++
- hm3dsem
- Reinforcement Learning
- UC Berkeley
- CS285
- deep learning
- 강화학습
- 머신러닝
- MySQL
- 딥러닝
- Python
- YoLO
- BFS
- CNN
- LSTM
- machine learning
- dynamic programming
- r-cnn
- Today
- Total
JINWOOJUNG
[ 핸즈온 머신러닝 ] 2. 머신러닝 프로젝트 처음부터 끝까지...3(Model 선정) 본문
본 포스팅은 Hands-On Machine Learning with Scikit-Learn, Keras & TensorFlow 2판을 토대로
공부한 내용을 정리하기 위한 포스팅입니다.
해당 도서에 나오는 Source Code 및 자료는 GitHub를 참조하여 진행하였습니다.
https://codingalzi.github.io/handson-ml2/
핸즈온 머신러닝
머신러닝/딥러닝 기초 지식 제공
codingalzi.github.io
.
https://jinwoo-jung.tistory.com/96
[ 핸즈온 머신러닝 ] 2. 머신러닝 프로젝트 처음부터 끝까지...2(Data 전처리)
본 포스팅은 Hands-On Machine Learning with Scikit-Learn, Keras & TensorFlow 2판을 토대로공부한 내용을 정리하기 위한 포스팅입니다. 해당 도서에 나오는 Source Code 및 자료는 GitHub를 참조하여 진행하였습니
jinwoo-jung.com
Model 선정
Train Set을 만들었으니 이제 Model을 선정 해 보자. 우선 가장 간단한 선형 모델부터 학습시켜 보자.
# Model 선택
from sklearn.linear_model import LinearRegression
st_LinearModel = LinearRegression()
st_LinearModel.fit(st_FinalTrainDataset, st_TrainSetLable)
st_TmpTestData = st_TrainSet.iloc[:5000]
st_TmpTestDataLabel = st_TrainSetLable.iloc[:5000]
st_FinalTmpTestData = full_pipeline.fit_transform(st_TmpTestData)
print("예측: ", st_LinearModel.predict(st_FinalTmpTestData)[:5])
print("정답: ", list(st_TmpTestDataLabel)[:5])
학습한 모델을 Train Set의 일부로 예측시켜 봤다. 범주형 특성을 One-Hot Encoding 시키는 과정에서, 만약에 Train Set의 일부가 4개의 특성으로만 존재한다면, 학습시킨 모델의 Input과 에러나기 때문에 Sub Train Set을 5000개로 선정 후 예측과 정답의 결과 비교는 5개만 진행하였다.

예측 결과를 바탕으로 선형 회귀 모델의 RMSE를 측정 해 보자.
st_ModelPredictResult = st_LinearModel.predict(st_FinalTmpTestData)
f32_RMSE = mean_squared_error(st_TmpTestDataLabel, st_ModelPredictResult)
f32_RMSE = np.sqrt(f32_RMSE)
print("RMSE: ", f32_RMSE)
RMSE는 $67,283으로 median_income이 $120,00~$265,000 범위에 대부분 분포해 있다는 것을 고려하면 좋지 않은 결과이다.
이는 모델이 훈련 데이터에 과소적합된 사례로, 특성딜이 좋은 예측을 만들 만큼 충분한 정보를 제공하지 못했거나, 모델이 충분히 강력하지 못한 상황이다.
단순히 복잡한 모델로 선정하면 해결할 수 있을까?
Input을 다시 고려 해 보자. 우리는 Train Set 중 일부를 테스트 하는 상황이다. 복잡한 모델(DecisionTree)을 기반으로 RMSE를 계산하면 0이 되는데(실제론 되야 하는데 안되서 글로 남김..아마 책에서 제시하는 TrainSet과의 차이로 인해서!?) 이는 Model이 Train Set에 Overfitting 되었기에 발생하는 결과이다. 실제로 구한 RMSE는 아래와 같다.

교차 검증
k-겹 교차 검증(k-fold cross-validation)
fold라고 불리는 10개의 SubSet으로 TrainSet을 분리시킨다. 이후, DecisionTree Model을 10번 훈련 시키는데, 각 훈련마다 서로 다른 fold를 선택하여 평가하고, 나머지 fold로 훈련시킨다.

생각보다 결과가 좋지 않으며, 심지어 선형 모델보다 더 낮은 성능을 보임을 확인할 수 있다.

실제로 선형회귀 모델의 점수를 계산 해 보면 DecisionTree Model이 Overfitting 되어 선형 모델보다 성능이 안좋음을 확인할 수 있다.
마지막으로 RandomForestRegressor Model을 시도해 보자. RandomForest는 특성을 무작위로 선택해서 더 많은 DecisionTree를 만들고, 그 예측을 평균 내는 방식으로 동작한다. 이처럼, 여러 다른 모델을 모아서 하나의 모델을 만드는 것을 앙상블 학습이라고 하며, 머신러닝 알고리즘 성능 향상의 방법 중 하나이다.
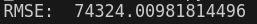

RandomForest Model이 다른 모델보다 훨씬 더 좋은 성능을 보임을 확인할 수 있다. 하지만, RMSE 가 훨씬 더 높은 것으로 보아, Validation에 대한 점수가 더 큼으로 모델이 TrainSet에 Overfitting 될 확률이 높다.
이처럼 다양한 Model을 시도하는 것도 좋지만, 각 Model의 세부적인 HyperParameter 조정도 요구된다.
모델 세부 튜닝
그리드 탐색
HyperParameter는 직접 조절하여 최상의 성능을 보이는 HyperParameter를 찾아야 한다. 하지만, GridSearchCV를 통해 구하고자 하는 HyperParameter와 테스트 하고자 하는 값만 입력하면, 가능한 모든 HyperParameter의 조합에 대하여 교차 검증을 사용하여 평가할 수 있다.
from sklearn.model_selection import GridSearchCV
st_RandomForest = RandomForestRegressor()
st_Parameter = [
# 총 12(=3×4)개의 하이퍼파라미터 조합 시도
{'n_estimators': [3, 10, 30], 'max_features': [2, 4, 6, 8]},
# bootstrap은 False로 하고 총 6(=2×3)개의 조합 시도
{'bootstrap': [False], 'n_estimators': [3, 10], 'max_features': [2, 3, 4]},
]
# 5-겹 교차 검증 시도. 따라서 총 (12+6)*5=90번의 훈련 진행
st_GridSearch = GridSearchCV(st_RandomForest, st_Parameter, cv=5,
scoring='neg_mean_squared_error',
return_train_score=True)
st_GridSearch.fit(st_FinalTrainDataset, st_TrainSetLable)
각각의 HyperParameter는 생각하지 말고, 어떻게 동작하는지만 생각 해 보자. 첫번째 조합은 n_estimators, max_features HyperParameter의 조합인 12가지와, bootstrap은 False로 설정한 후, n_estimators, max_features HyperParameter의 조합인 6개 총 18개의 조합을 탐색하는데, 이때 각각 5번 모델을 훈련시킨다. 따라서 총 90번의 학습이 진행되고, 최적의 조합을 추출할 수 있다.
print(st_GridSearch.best_params_) # 최상의 성능을 가지는 HyperParameter 조합
print(st_GridSearch.best_estimator_) # 최상의 성능을 가지는 모델
cvres = st_GridSearch.cv_results_
# 각 HyperParameter 조합에 대한 RMSE Score
for mean_score, params in zip(cvres["mean_test_score"], cvres["params"]):
print(np.sqrt(-mean_score), params)
위 예시의 경우 bootstrap : True, max_features : 8, n_estimators : 30인 경우가 최상의 모델이며, 기본 HyperParameter로 설정한 Model 보다 훨씬 더 좋은 성능을 지니는 모델을 찾을 수 있다. 하지만, max_features : 8, n_estimators : 30은 설정한 두 HyperParameter 조합의 최댓값이기에 더 다양한 경우의 수를 설정한다면, 더 좋은 성능을 지니는 모델을 찾을 수 있을 것이다.
랜덤 선택
GirdSearch의 경우 작은 조합(경우의 수)에 더 효과적으로 동작한다. 하지만, 탐색할 범위(조합)이 더 커지면, RandomizedSearchCV를 사용하는 것이 더 효과적이다. 동작 방식은 유사하나, 가능한 모든 조합을 시도하고, 각 조합마다 지정한 횟수만큼 평가한다.
from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import randint
param_distribs = {
'n_estimators': randint(low=1, high=200),
'max_features': randint(low=1, high=8),
}
st_RandomForest = RandomForestRegressor()
st_RamdomizedSearch = RandomizedSearchCV(st_RandomForest, param_distributions=param_distribs,
n_iter=10, cv=5, scoring='neg_mean_squared_error', random_state=42)
st_RamdomizedSearch.fit(st_FinalTrainDataset, st_TrainSetLable)
cvres = st_RamdomizedSearch.cv_results_
for mean_score, params in zip(cvres["mean_test_score"], cvres["params"]):
print(np.sqrt(-mean_score), params)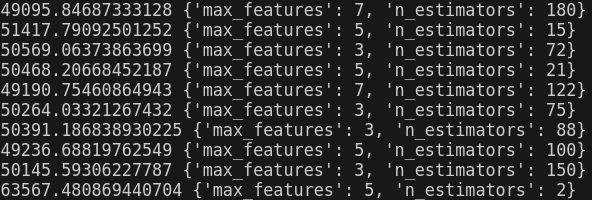
GridSearch 기반으로 찾은 최적의 HyperParameter 조합은 bootstrap : True, max_features : 8, n_estimators : 30이다. 하지만, RandomizedSearchCV를 통해서 구한 최상의 모델의 HyperParameter 조합은 bootstrap : True, max_features : 7, n_estimators : 180으로, 모델의 성능도 훨씬 더 좋음을 확인할 수 있다.
앙상블 방법
모델을 튜닝하는 방법은 결정 트리의 앙상블인 RandomForest와 같이 최상의 모델을 연결하는 앙상블 방법이다. 자세한 것은 추후 학습 예정.
최상의 모델과 오차 분석
최상의 모델을 분석하는 것은, 문제에 대한 이해와 각 특성의 중요도를 분석할 수 있다.
FeatureImportance = st_RamdomizedSearch.best_estimator_.feature_importances_
print(FeatureImportance)
각 특성마다의 중요도를 뽑아냈는데, 이렇게 보면 모르기에 각각의 특성 이름과 함께 출력 해 보자.
FeatureImportance = st_RamdomizedSearch.best_estimator_.feature_importances_
ars_ExtraAttribs = ["rooms_per_hhold", "pop_per_hhold", "bedrooms_per_room"] # 추가적으로 계산한 특성
st_RangeAttribs = full_pipeline.named_transformers_["cat"] # 범주형 특성
ars_OneHotAttribs = list(st_RangeAttribs.categories_[0]) # One-Hot Encoding을 한 범주형 특성
ars_Attributes = num_attribs + ars_ExtraAttribs + ars_OneHotAttribs
각각의 특성과, One-Hot Encoding 한 범주형 특성의 이름들을 불러와, 각 특성의 중요도와 묶어서 출력하도록 하였다.
위 정보를 바탕으로, 각 특성의 중요도를 분석할 수 있는데, 예를들면 ocean_proximity의 범주형 특성 중 "INLAND"만 중요도가 높고 나머지는 불필요함을 확인할 수 있다.
테스트 세트로 시스템 평가하기
최상의 성능을 보이는 모델을 평가해보자. 앞서 나눠둔 TestSet을 기반으로 진행한다.
st_FinalModel = st_RamdomizedSearch.best_estimator_
st_TestSetX = st_TestSetTmp.drop("median_house_value", axis=1)
st_TestSetY = st_TestSetTmp["median_house_value"].copy()
st_TestSetX = full_pipeline.transform(st_TestSetX)
st_Prediction = st_FinalModel.predict(st_TestSetX)
f64_RMSE = np.sqrt(mean_squared_error(st_TestSetY, st_Prediction))
print(f64_RMSE)
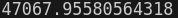
하지만 단순히 RMSE Value를 기반으로 해당 모델을 통해 론칭을 할 수 있을까? 론칭할 수 있을만큼 추정값이 얼마나 정확한지를 알고 싶다. 이때, 일반화 오차의 95% 신뢰 구간을 계산하면 되는데, scipy.stats.t.interval()를 사용하면 된다.
여기서 일반화 오차(Generation Error)는 학습된 모델이 새로운 데이터에 대하여 얼마나 잘 예측하는지를 나타내는 지표로, 일반화 오차가 작을수록 모델은 새로운 데이터에 대하여 더 잘 예측하는 일반화가 잘 된 모델임을 의미한다.
실제 계산결과 array([45685.10470776, 49691.25001878])로, 일반화 오차가 해당 범위 내에 있을 확률이 95%임을 의미한다.
'핸즈온머신러닝' 카테고리의 다른 글
| [ 핸즈온 머신러닝 ] 3. 분류...2(MultiClass Classifier) (2) | 2024.09.05 |
|---|---|
| [ 핸즈온 머신러닝 ] 3. 분류...1(Binary Classifier) (14) | 2024.08.29 |
| [ 핸즈온 머신러닝 ] 2. 머신러닝 프로젝트 처음부터 끝까지...2(Data 전처리) (0) | 2024.08.20 |
| [ 핸즈온 머신러닝 ] 2. 머신러닝 프로젝트 처음부터 끝까지...2(Data 전처리 1) (0) | 2024.08.20 |
| [ 핸즈온 머신러닝 ] 2. 머신러닝 프로젝트 처음부터 끝까지...1(데이터 분석) (0) | 2024.08.18 |




