| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- dynamic programming
- CNN
- RL
- NLP
- AlexNet
- dfs
- DP
- hm3d
- opencv
- 머신러닝
- Reinforcement Learning
- CS285
- LSTM
- GIT
- 백준
- hm3dsem
- Python
- machine learning
- UC Berkeley
- YoLO
- C++
- r-cnn
- MySQL
- ubuntu
- 그래프 이론
- 딥러닝
- image processing
- deep learning
- 강화학습
- BFS
- Today
- Total
JINWOOJUNG
[RL] CS285: Lecture 06. Actor-Critic Algorithms(2) 본문
[RL] CS285: Lecture 06. Actor-Critic Algorithms(2)
Jinu_01 2026. 1. 29. 15:10본 포스팅은 UC Berkeley 에서 진행된 CS285: Deep Reinforcement Learning, Decision Making and Control
강의자료 및 강의를 기반으로 공부한 내용을 정리하는 포스팅입니다.
https://jinwoo-jung.tistory.com/177
[RL] CS285: Lecture 06. Actor-Critic Algorithms(1)
본 포스팅은 UC Berkeley 에서 진행된 CS285: Deep Reinforcement Learning, Decision Making and Control강의자료 및 강의를 기반으로 공부한 내용을 정리하는 포스팅입니다.https://jinwoo-jung.tistory.com/176 [RL] CS285: Lecture
jinwoo-jung.com
Actor-Critic Design Decisions
RL algorithm을 공부했다면, 이제 구체적 코드로 Instantiate하는 과정이 요구된다.
Architecture design
우리가 학습해야 할 대상은 Policy $\pi$(Actor)와 Value function $V$(Critic) 2가지이다. 만약 각각을 서로 다른 Network로 설계한다면 매우 간단하고 안정적이지만, Feature를 공유하지 못하는 단점이 있다. 만약 Feature를 공유하도록 하나의 Network로 설계한다면 매우 효율적이나, Policy와 Value function 각각이 서로 다른 Gradient를 가지기에 복잡성이 커진다.

Online/Offline learning
다음으론 Online/Offline learning을 결정해야 한다.
Online learning은 데이터를 수집하면서 동시에 학습함을 의미한다. Policy가 바뀌면 바로 환경에서 행동도 바뀌게 되는 것으로, On-policy 성질이 강하다.
Offline learning은 이미 모아둔 데이터셋으로만 학습함을 의미한다. 환경과 추가적인 상호작용없이, 기존의 Policy로 취득한 데이터셋으로 Policy를 업데이트 하게 된다.
Online actor-critic algorithm을 살펴보면, 현재 Policy를 기반으로 행동하면서 데이터를 수집함을 확인할 수 있다. Update 과정 역시 Monte Carlo가 아닌 TD 방식이기에 Online으로 학습이 가능하다. 하지만 TD 방식이기에 Variance가 크므로 Batch로 평균을 내면 Gradient를 안정화시킬 수 있다.

Batch 단위로 동작하는 과정에서 Synchronized 여부를 결정해야 한다.
Synchronized는 Batch로 모아서 한번에 Update 하는 방식이다. 모든 Workers가 동일한 $\phi, \pi$를 기반으로 환경과 상호작용하여 데이터를 수집한 뒤 Batch update를 진행한다. 이는 Variance를 줄이고 안정적인 학습이 가능하나, Workers의 동작 속도에 따른 병목 현상이 발생할 수 있다.
Asynchronous는 기다림 없이 각 Worker가 데이터를 수집해 준비되는데로 Update 하는 방식이다. 이는 CPU/GPU 자원의 효율성과 서로 다른 정책으로 인한 탐험의 다양성이 있지만, 동일한 Parameter를 기반으로 수행된 결과가 아닐 수 있으며, 공유중인 최신의 Parameter가 아닌 Old parameter를 기반으로 취득될 수 있다.

그렇다면 아예 On-policy라는 가정을 제외하면 되지 않을까? Off-policy actor-critic을 살펴보면 Replay buffer를 사용하게 된다. 즉, Update 과정에서 최근에 얻은 데이터가 아닌 Replay buffer에 담긴 transitions를 기반으로 Update를 하게 된다. 이는 Older policy에 의한 Transition이 담겨져 있기 때문에 Off-policy 인 것이다.
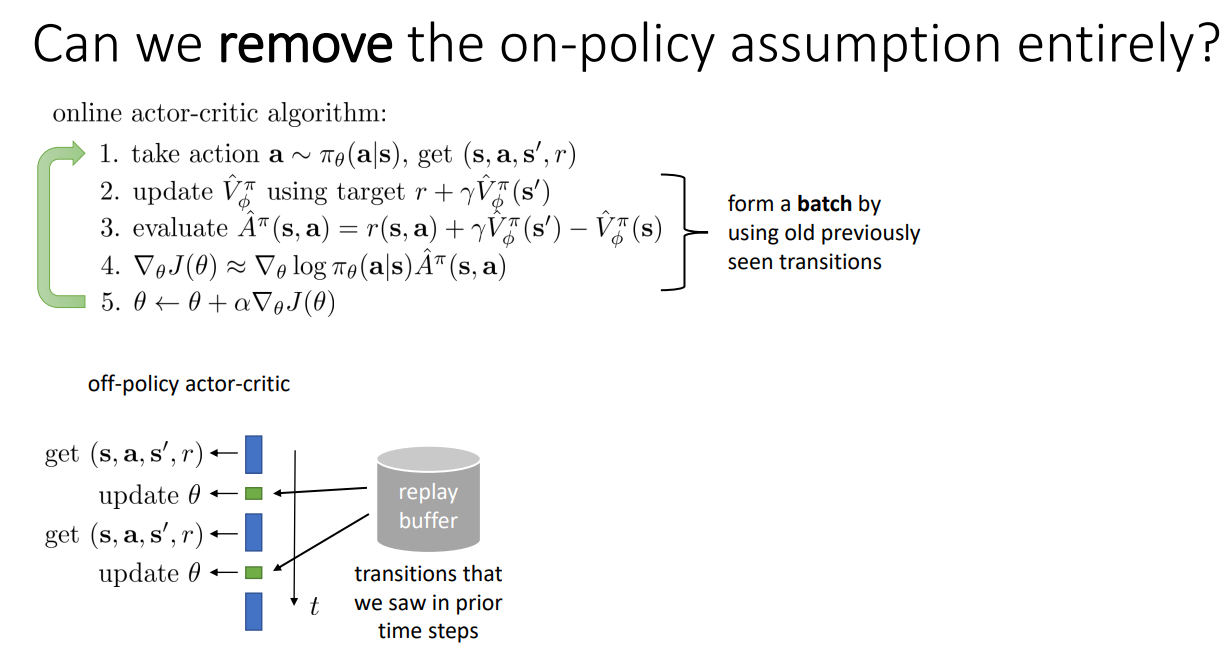
하지만, 기존의 Off-policy 처럼 Algorithm을 수정하면 몇가지 에러 사항이 있다. 이는 Actor, Critic을 Fitting 하는 과정에서 발생하게 된다.

Fixing the value function(Critic)
먼저 Value function을 Fitting하는 과정을 살펴보자. 이때 우리가 Target으로하는 $y_i$는 $\pi$에서 샘플된 Action이여야 한다.
$$y_i = r_i + \gamma\hat{V}_\phi^\pi$$
하지만, 현재 Action을 포함하는 데이터는 Replay buffer $\mathcal{R}$로 부터 취득되기 때문에 현재 정책 $\pi$를 기반으로 된 것이 아니기에 정확한 Target value가 아니다. 즉, 현재 Policy 기반이 아닌 여러 Policy가 섞인 Replay buffer로 부터 취득되기에 정확한 Value를 구할 수 없다.
현재 Policy에 의한 $a_t$가 아닌 것이 문제였기에 이를 보완하려면 $a_t$ 역시 주어지는 Q-function을 이용할 수 있을 것이다. Value function 식을 조금 수정하면 다음과 같이 전개할 수 있다.
$$V^\pi(s_t) = E_{\pi_\theta} \left [ \sum_{t'=t}^{T} r(s_{t'}, a_{t'}) | s_t \right ]$$
이때, 통상적으로 많이 사용되는 조건부 기대값의 법칙을 활용하면 행동에 대해 기대값을 한 번 분리할 수 있다.
$$V^\pi(s_t) = E_{a_t \sim \pi(a_t|s_t)} \left [ E_{\pi_\theta} \left [ \sum_{t'=t}^{T} r(s_{t'}, a_{t'}) | s_t, a_t \right ] \right ] $$
이때, 안쪽 기대값은 Q-function과 동일하므로, 다음과 같다.
$$Q^\pi(s_t,a_t) = \left [ \sum_{t'=t}^{T} r(s_{t'}, a_{t'} | s_t, a_t \right ] $$
$$V^\pi(s_t) = E_{a_t \sim \pi(a_t|s_t)} \left [ Q^\pi(s_t) \right ]$$
따라서 우리는 Value function이 아닌 Q-function을 Target으로 설정할 수 있으며, Loss function $\mathcal{L}$역시 다음과 같이 수정할 수 있다.

Fixing the policy update(Actor)
이번에는 Policy를 Fitting하는 과정을 살펴보자. Objective function의 Gradient를 계산하는 수식은 다음과 같다.
$$\nabla_\theta J(\theta) \approx \frac{1}{N} \sum_i \nabla_\theta log \pi_\theta (a_i|s_i) \hat(A)^\pi (s_i, a_i)$$
우리는 Replay buffer로부터 $s_i, a_i$를 꺼내고 있지, 현재 정책 $\pi_\theta$가 선택한 행동이 아니기 때문에, Policy gradient의 전제가 깨지게 된 것이다. 그렇다면 이를 해결하는 방법은? Data의 Action을 사용하지 않고, 현재의 Policy로부터 Action을 뽑아 활용하면 된다. 따라서 다음과 같이 수정할 수 있다.

최종적으로 수정된 Algorithm은 다음과 같다.

그렇다면 더 수정해야할 부분이 없을까? Off-policy 특성 상 $s_i$는 Replay buffer로 부터 취득된 상태이지, 현재 정책 $\pi_\theta$로부터 취득된 상태가 아니다. 따라서 State 분포가 조금 어긋나지만, 우리의 목적은 현재 정책이 실제로 방문하는 States에서의 성능을 최적화 하는 것이지만, 실제로 더 넓은 State 분포에서 평균적으로 좋도록 학습되기에 넘어가자.

Critics as Baselines
지금까지는 Actor-Critic algorithms으로써 Value function을 Critic으로 칭하면서 살펴보았다. 그렇다면 Policy gradient에서 Value function을 Baseline으로써 활용하는 방법을 살펴보자.
먼저 Actor-critic과 Policy gradient의 차이는 다음과 같다. Actor-critic은 Critic으로 Variance를 낮췄지만, Critic의 정확성으로 인해 Biased 된다는 단점이 있었다. Policy gradient는 Unbiased 된 Baseline으로 Variance를 낮췄찌만, 여전히 Single sample을 활용하기에 Variance가 크다는 단점이 있었다.

그렇다면 두 식의 장점만을 가져와 혼합한다면?
Baseline을 통해 Unbiased 하면서 동시에 Critic을 활용하므로 Variance도 낮출 수 있을 것이다.

여기서 조금 더 낮출 수 있는 방법이 Value function이 아닌 Q-function을 활용하는 것이다. State뿐만 아니라 Action까지 주어졌으니, 만약 Critic이 정확하다면 더 Return에 가까운 값을 가지므로 Variance가 작아질 것이다.
강의에선 잘 다루지 않았지만, 궁금하면 Q-Prop 논문을 찾아보면 좋을 것 같다.

N-step returns
Monte Carlo에서는 Single-sample을 활용하기 때문에 Variance가 매우 크다는 것을 배웠었다. 그렇다면 끝까지 가는것이 아닌 $n$ step만 살펴보고, 나머지는 Value function을 통해 예측한 값을 사용하면 어떻게 될까?
이러한 아이디에서 나온 것이 바로 n-step returns이다. 이는 실제 값을 사용해 Bias도 낮춤과 동시에 Value function을 통해 Variance도 줄일 수 있다. 하지만 여전히 $n$이 커지면 Variance가 증가하게된다.

Generalized advantage estimation(GAE)
마지막으로 살펴볼 것은 GAE이다. 앞선 n-step return은 $n$을 직접 설정해야 한다. 그렇다면, 모든 $n$에 대해 구한 값을 적절히 사용해서 Weighted combination을 하면 어떨까? GAE에서는 전부 다 사용하는 대신에 이처럼 가중치를 줌으로써 짧은 $n$을 더 신뢰할 수 있도록 하였다. 따라서 $\lambda$는 또 하나의 Discount factor처럼 동작하게 된다.

'Reinforcement Learning' 카테고리의 다른 글
| [RL] CS285: Lecture 06. Actor-Critic Algorithms(1) (0) | 2026.01.29 |
|---|---|
| [RL] CS285: Lecture 05. Policy gradients(2) (0) | 2026.01.28 |
| [RL] CS285: Lecture 05. Policy gradients(1) (0) | 2026.01.28 |
| [RL] CS285: Lecture 04. Introduction to Reinforcement Learning(2) (0) | 2026.01.27 |
| [RL] CS285: Lecture 04. Introduction to Reinforcement Learning(1) (0) | 2026.01.27 |




